গন্তব্যে পৌঁছাতে ন্যূনতম প্রাথমিক পয়েন্ট

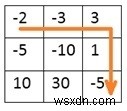
প্রদত্ত গ্রিডের উপরের-বাম কোণ থেকে শুরু করতে, একজনকে নীচে-ডান কোণায় পৌঁছাতে হবে৷ গ্রিডের প্রতিটি ঘরে একটি সংখ্যা রয়েছে, সংখ্যাটি ধনাত্মক বা ঋণাত্মক হতে পারে। যখন ব্যক্তি একটি কক্ষে (i, j) পৌঁছায় তখন তার কাছে থাকা টোকেনের সংখ্যা সেই কক্ষের মানগুলির সাথে বৃদ্ধি বা হ্রাস হতে পারে। যাত্রা সম্পূর্ণ করার জন্য আমাদের ন্যূনতম সংখ্যক প্রাথমিক টোকেন প্রয়োজন।

কিছু নিয়ম আছে -

• আমরা হয় ডানে বা নীচে যেতে পারি।
• আমাদের মোট টোকেন যদি (i, j) এর মান কম হয় তাহলে আমরা একটি কক্ষে (i, j) যেতে পারি না।
• আমাদের ন্যূনতম ইতিবাচক পয়েন্ট নিয়ে গন্তব্যে পৌঁছাতে হবে।

ইনপুট এবং আউটপুট

Input:
The token for each room as a matrix.
-2  -3  3
-5 -10  1
10  30 -5

Output:
The minimum token required to start the journey. For this example, the required token is 7.

অ্যালগরিদম

minInitTokens(matrix)

ইনপুট: প্রতিটি রুমের জন্য টোকেন ম্যাট্রিক্স।

আউটপুট - গন্তব্যে স্টার্ট পয়েন্টে পৌঁছানোর জন্য ন্যূনতম টোকেন প্রয়োজন।

Begin
   define matrix minToken of size same as matrix
   m := number of rows in matrix
   n := number of columns in matrix

   if matrix[m-1, n-1] > 0, then
      minToken[m-1, n-1] := 0
   else
      minToken[m-1, n-1] := 1 + absolute value of matrix[m-1, n-1]

   for i := m-2 down to 0, do
      minToken[i, n-1] := maximum of 1 and (minToken[i+1, n-1]-matrix[i,n-1])
   done

   for j := n-2 down to 0, do
      minToken[m-1, j] := maximum of 1 and (minToken[m-1, j+1]-matrix[m-1, j])
   done

   for i := m-2 down to 0, do
      for j := n-2 down to 0, do
         rem := minimum of minToken[i+1, j] and minToken[i, j+1]
         minPoint[i, j] := maximum of 1 and (rem – matrix[i,j])
      done
   done

   return minToken[0, 0]
End

উদাহরণ

#include<iostream>
#include<cmath>
#define ROW 3
#define COL 3
using namespace std;

int tokens[ROW][COL] = {
   {-2,-3,3},
   {-5,-10,1},
   {10,30,-5}
};

int max(int a, int b) {
   return (a>b)?a:b;
}

int minInitPoints() {
   int minToken[ROW][COL];
   int m = ROW, n = COL;
   
   minToken[m-1][n-1] = tokens[m-1][n-1] > 0? 1: abs(tokens[m-1][n-1]) + 1;
   
   for (int i = m-2; i >= 0; i--)    //from last row to first row, fill points
      minToken[i][n-1] = max(minToken[i+1][n-1] - tokens[i][n-1], 1);
   
   for (int j = n-2; j >= 0; j--)    //fill last column to first column, fill points
      minToken[m-1][j] = max(minToken[m-1][j+1] - tokens[m-1][j], 1);

   for (int i=m-2; i>=0; i--) {
      for (int j=n-2; j>=0; j--) {
         int remPoint = min(minToken[i+1][j], minToken[i][j+1]);    //calculate remaining points
         minToken[i][j] = max(remPoint - tokens[i][j], 1);
      }
   }
   return minToken[0][0];
}

int main() {
   cout << "Minimum Points Required: " << minInitPoints();
}

আউটপুট

Minimum Points Required: 7