ধরুন আমরা d দিনের মধ্যে কাজের একটি তালিকা নির্ধারণ করতে চাই। কাজগুলি নির্ভরশীল তাই, i-th টাস্কে কাজ করতে, আমাদের সমস্ত কাজ j শেষ করতে হবে যেখানে 0 <=j
আমাদের প্রতিদিন অন্তত একটি কাজ শেষ করতে হবে। একটি টাস্ক শিডিউলের অসুবিধা আসলে d সংখ্যার প্রতিটি দিনের অসুবিধার সমষ্টি। একটি দিনের অসুবিধা হল সেই দিনে করা একটি কাজের সর্বোচ্চ অসুবিধা৷
তাই আমাদের কাছে টাস্কডিফিকালটি নামক পূর্ণসংখ্যার একটি অ্যারে রয়েছে এবং একটি পূর্ণসংখ্যা ডি। i-th কাজের অসুবিধা হল টাস্ক ডিফিকাল্টি[i]। আমাদের একটি টাস্ক শিডিউলের ন্যূনতম অসুবিধা খুঁজে বের করতে হবে। যদি আমরা কাজের জন্য একটি সময়সূচী খুঁজে না পাই, তাহলে -1 ফিরে আসুন।
সুতরাং, যদি ইনপুট টাস্ক ডিফিকালটি =[6,5,4,3,2,1], d =2,
তাহলে আউটপুট হবে 7, যেমন 1 দিনে আমরা প্রথম 5 টি কাজ শেষ করতে পারি, মোট অসুবিধা 6। এখন 2 য় দিনে আমরা শেষ কাজ শেষ করতে পারি, মোট অসুবিধা 1, তাই সময়সূচীর অসুবিধা হবে 6 + 1 =7।
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
একটি ফাংশন সল্ভ() সংজ্ঞায়িত করুন, এটি একটি অ্যারে v, idx, k, একটি 2D dp,
যদি idx v এর আকারের সমান হয় এবং k 0 এর সমান হয়, তাহলে −
ফেরত 0
যদি k <0 বা idx v এবং k> 0 এর আকারের সমান হয়, তাহলে −
1^6
যদি dp[idx, k] -1 এর সমান না হয়, তাহলে −
dp[idx, k]
maxVal :=0
ret :=inf
আরম্ভ করার জন্য i :=idx, যখন i <আকার v এর, আপডেট করুন (i 1 দ্বারা বাড়ান), করবেন −
maxVal :=সর্বাধিক v[i] এবং maxVal
ret :=ret এবং maxVal + সমাধানের সর্বনিম্ন (v, i + 1, k - 1, dp)
dp[idx, k] :=ret
রিটার্ন রিটার্ন
প্রধান পদ্ধতি থেকে নিম্নলিখিতগুলি করুন -
n :=j
যদি d> n হয়, তাহলে −
রিটার্ন -1
n x (d + 1) আকারের একটি 2D অ্যারে dp সংজ্ঞায়িত করুন এবং এটি -1 দিয়ে পূরণ করুন
রিটার্ন সলভ (j, 0, d, dp)
আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -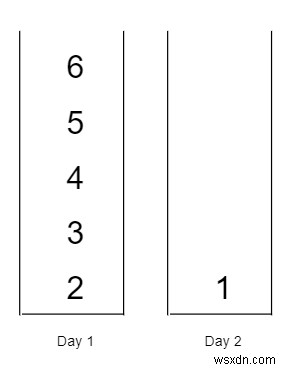
উদাহরণ
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int solve(vector<int>& v, int idx, int k, vector<vector<int> >&
dp){
if (idx == v.size() && k == 0)
return 0;
if (k < 0 || idx == v.size() && k > 0)
return 1e6;
if (dp[idx][k] != -1)
return dp[idx][k];
int maxVal = 0;
int ret = INT_MAX;
for (int i = idx; i < v.size(); i++) {
maxVal = max(v[i], maxVal);
ret = min(ret, maxVal + solve(v, i + 1, k - 1, dp));
}
return dp[idx][k] = ret;
}
int minDifficulty(vector<int>& j, int d){
int n = j.size();
if (d > n)
return -1;
vector<vector<int> > dp(n, vector<int>(d + 1, -1));
return solve(j, 0, d, dp);
}
};
main(){
Solution ob;
vector<int> v = {6,5,4,3,2,1};
cout << (ob.minDifficulty(v, 2));
} ইনপুট
{6,5,4,3,2,1}, 2 আউটপুট
7


