এই প্রবন্ধে, আমরা প্রদত্ত সমস্যার বিবৃতিটি সমাধান করার জন্য সমাধান এবং পদ্ধতি সম্পর্কে শিখব।
সমস্যা বিবৃতি
পূর্ণসংখ্যা n এবং d দেওয়া আছে। আমাদের d দ্বারা বিভাজ্য ক্ষুদ্রতম n-সংখ্যার সংখ্যা খুঁজে বের করতে হবে।
পন্থা
1. প্রথমে এখন আমরা MIN গণনা করি :ক্ষুদ্রতম n-সংখ্যা (1000...n-বার)
2. এখন, যদি MIN % X 0 হয়, ans =MIN
3. অন্য, উত্তর =(MIN + X) - ((MIN + X) % X))
এর কারণ হল [MIN...MIN+X] পরিসরে একটি সংখ্যা থাকবে যা d দ্বারা বিভাজ্য।
এখন এর বাস্তবায়ন দেখি -
উদাহরণ
def answer(n, d): # Computing MAX Min = pow(10, d-1) if(Min%n == 0): return (Min) else: return ((Min + n) - ((Min + n) % n)) n = 83 d = 5 print(answer(n, d))
আউটপুট
10043
সমস্ত ভেরিয়েবলগুলিকে গ্লোবাল ফ্রেমে ঘোষণা করা হয়েছে যেমন নীচে দেওয়া চিত্রে দেখানো হয়েছে −
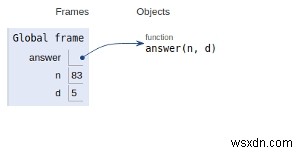
উপসংহার
এই নিবন্ধে, আমরা X দ্বারা বিভাজ্য ক্ষুদ্রতম K সংখ্যার সংখ্যা খুঁজে বের করার পদ্ধতি সম্পর্কে শিখেছি


