n-তম ফিবোনাচি সংখ্যার জন্য পাইথন প্রোগ্রাম

এই নিবন্ধে, আমরা nম ফিবোনাচি সংখ্যা গণনা করব।

একটি ফিবোনাচি সংখ্যা নীচে দেওয়া পুনরাবৃত্তি সম্পর্ক দ্বারা সংজ্ঞায়িত করা হয় −

Fn = Fn-1 + Fn-2

এর সাথে F₀ =0 এবং F₁ =1.

প্রথমত, কয়েকটি ফিবোনাচি সংখ্যা হল

0,1,1,2,3,5,8,13,..................

আমরা ফিবোনাচি সংখ্যা গণনা করতে পারি পুনরাবৃত্তি এবং গতিশীল প্রোগ্রামিং পদ্ধতি ব্যবহার করে।

এখন পাইথন স্ক্রিপ্ট আকারে বাস্তবায়ন দেখি

পদ্ধতি 1:পুনরাবৃত্তি পদ্ধতি

উদাহরণ

#recursive approach
def Fibonacci(n):
   if n<0:
      print("Fibbonacci can't be computed")
   # First Fibonacci number
   elif n==1:
      return 0
   # Second Fibonacci number
   elif n==2:
      return 1
   else:
      return Fibonacci(n-1)+Fibonacci(n-2)
# main
n=10
print(Fibonacci(n))

আউটপুট

34

ঘোষিত সমস্ত ভেরিয়েবলের সুযোগ নীচে দেখানো হয়েছে৷

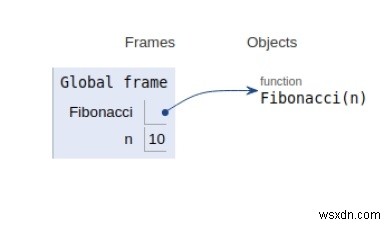
পদ্ধতি 2:ডায়নামিক প্রোগ্রামিং পদ্ধতি

উদাহরণ

#dynamic approach
Fib_Array = [0,1]
def fibonacci(n):
   if n<0:
      print("Fibbonacci can't be computed")
   elif n<=len(Fib_Array):
      return Fib_Array[n-1]
   else:
      temp = fibonacci(n-1)+fibonacci(n-2)
      Fib_Array.append(temp)
      return temp
# Driver Program
n=10
print(fibonacci(n))

আউটপুট

34

ঘোষিত সমস্ত ভেরিয়েবলের সুযোগ নীচে দেখানো হয়েছে

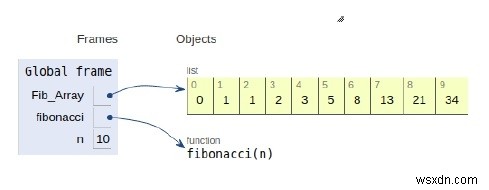
উপসংহার

এই নিবন্ধে, আমরা পুনরাবৃত্তি এবং গতিশীল প্রোগ্রামিং পদ্ধতি ব্যবহার করে nম ফিবোনাচি সংখ্যার গণনা সম্পর্কে শিখেছি।