nম কাতালান নম্বরের জন্য পাইথন প্রোগ্রাম

এই নিবন্ধে, আমরা nম কাতালান সংখ্যা গণনা সম্পর্কে শিখব।

কাতালান সংখ্যা প্রাকৃতিক সংখ্যার একটি ক্রম যা পুনরাবৃত্তিমূলক সূত্র দ্বারা সংজ্ঞায়িত করা হয় −

$$C_{0}=1\:and\:C_{n+1}=\displaystyle\sum\limits_{i=0}^n C_{i}C_{n-i} \:n\geq0;$$ এর জন্য

n =0, 1, 2, 3, … এর জন্য প্রথম কয়েকটি কাতালান সংখ্যা হল 1, 1, 2, 5, 14, 42, 132,429,............... ....

কাতালান সংখ্যাগুলি পুনরাবৃত্তি এবং গতিশীল প্রোগ্রামিং উভয়ের মাধ্যমেই প্রাপ্ত করা যেতে পারে৷ তাই আসুন তাদের বাস্তবায়ন দেখি৷

পদ্ধতি 1:পুনরাবৃত্তি পদ্ধতি

উদাহরণ

# A recursive solution
def catalan(n):
   #negative value
   if n <=1 :
      return 1
   # Catalan(n) = catalan(i)*catalan(n-i-1)
   res = 0
   for i in range(n):
      res += catalan(i) * catalan(n-i-1)
   return res
# main
for i in range(6):
   print (catalan(i))

আউটপুট

1
1
2
5
14
42

সমস্ত ভেরিয়েবল এবং রিকার্সিভ কলের সুযোগ নীচে দেখানো হয়েছে৷

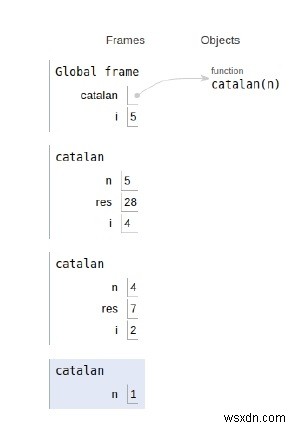
পদ্ধতি 2:ডায়নামিক প্রোগ্রামিং পদ্ধতি

উদাহরণ

# using dynamic programming
def catalan(n):
   if (n == 0 or n == 1):
      return 1
   # divide table
   catalan = [0 for i in range(n + 1)]
   # Initialization
   catalan[0] = 1
   catalan[1] = 1
   # recursion
   for i in range(2, n + 1):
      catalan[i] = 0
      for j in range(i):
         catalan[i] = catalan[i] + catalan[j] * catalan[i-j-1]
   return catalan[n]
# main
for i in range (6):
   print (catalan(i),end=" ")

আউটপুট

1
1
2
5
14
42

সমস্ত ভেরিয়েবল এবং রিকার্সিভ কলের সুযোগ নীচে দেখানো হয়েছে৷

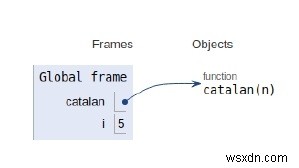
উপসংহার

এই নিবন্ধে, আমরা nম কাতালান সংখ্যা তৈরি করার পদ্ধতি সম্পর্কে শিখেছি।