জটিল সংখ্যার জন্য পাইথন প্রোগ্রাম

একটি ধনাত্মক সংখ্যার দুটি প্রকৃত মূল সবসময় থাকে। উদাহরণস্বরূপ, যদি x2 হয় 25, x হয় ±5। যাইহোক, x2 হলে -25 বাস্তব রুট নেই। যেকোনো ঋণাত্মক সংখ্যার বর্গমূল হল তার পরম মানের বর্গমূল যা একটি কাল্পনিক একক j =√−1 দ্বারা গুণিত হয়।

তাই √−25 =√25 𝑋−1 =√25 × √−1 =5j

একটি জটিল সংখ্যা বাস্তব এবং কাল্পনিক উপাদান নিয়ে গঠিত। এটি x+yj হিসাবে উপস্থাপিত হয়। x এবং y উভয়ই বাস্তব সংখ্যা। Y কাল্পনিক একক দ্বারা গুণ করলে জটিল সংখ্যার একটি কাল্পনিক অংশ হয়।

উদাহরণ:3+2j, 10-5.5J, 9.55+2.3j, 5.11e-6+4j

পাইথনের একটি অন্তর্নির্মিত জটিল ডেটা টাইপ রয়েছে। নিম্নরূপ আক্ষরিক উপস্থাপনা দ্বারা একটি জটিল সংখ্যা বস্তু তৈরি করা যেতে পারে -

>>> x = 2+3j
>>> type(x)

জটিল সংখ্যা বস্তুর দুটি বৈশিষ্ট্য আছে বাস্তব (বাস্তব উপাদান প্রদান করে) এবং imag (কাল্পনিক একক j বাদ দিয়ে কাল্পনিক উপাদান প্রদান করে)

>>> x.real
2.0
>>> x.imag
3.0

এটিতে কনজুগেট()ও আছে পদ্ধতি একটি জটিল সংখ্যার সংযোজনে বিপরীত চিহ্ন সহ একই বাস্তব উপাদান এবং কাল্পনিক উপাদান রয়েছে। তাই 2+3j এর সংযোজন হল 2-3j

>>> x.conjugate()
(2-3j)

পাইথনে বিল্ট-ইন কমপ্লেক্স() ফাংশন রয়েছে যা একটি জটিল সংখ্যা বস্তু প্রদান করে। ফাংশনটি দুটি পরামিতি নেয়, একটি বাস্তব এবং কাল্পনিক উপাদানের জন্য। এগুলি যেকোন সাংখ্যিক প্রকারের হতে পারে (int, float বা জটিল)

>>> complex(9,5)
(9+5j)
>>> complex(-6, -2.5)
(-6-2.5j)
>>> complex(1.5j, 2.5j)
(-2.5+1.5j)

যদি শুধুমাত্র একটি প্যারামিটার দেওয়া হয় তবে এটি বাস্তব উপাদান হিসাবে বিবেচিত হয়, কাল্পনিক উপাদানটি শূন্য বলে ধরে নেওয়া হয়।

>>> complex(15)
(15+0j)

ফাংশনটি আর্গুমেন্ট হিসাবে একটি স্ট্রিংও নিতে পারে যদি এতে সাংখ্যিক উপস্থাপনা থাকে।

>>> complex('51')
(51+0j)
>>> complex('1.5')
(1.5+0j)

জটিল সংখ্যার যোগ ও বিয়োগ পূর্ণসংখ্যা বা ভাসমান সংখ্যার অনুরূপ। বাস্তব এবং কাল্পনিক অংশ আলাদাভাবে যোগ/বিয়োগ করা হয়।

>>> a = 6+4j
>>> b = 3+6j
>>> a+b
(9+10j)
>>> a-b
(3-2j)

গুণের জন্য জটিল সংখ্যাটিকে দ্বিপদ হিসাবে বিবেচনা করুন এবং প্রথম সংখ্যার প্রতিটি পদকে দ্বিতীয় সংখ্যার প্রতিটি পদ দ্বারা গুণ করুন।

a = 6+4j
b = 3+2j
c = a*b
c = (6+4j)*(3+2j)
c = (18+12j+12j+8*-1)
c = 10+24j

পাইথন কনসোলে ফলাফল এটি যাচাই করে −

>>> a = 6+4j
>>> b = 3+2j
>>> a*b
(10+24j)

জটিল সংখ্যার বিভাজন নিম্নরূপ −

দুটি সংখ্যা হতে দিন

a =2+4j

b =1-2j

এবং আমরা a/b গণনা করতে চাই।

হর এর সংযোজক প্রাপ্ত করুন যা 1+2j

লব এবং হরকে সংযোজিত দ্বারা গুণ করুন বিভাজনের ফলাফল পেতে হর এর

c = a/b
c = (2+4j)*(1+2j)/(1-2j)(1+2j)
c = (2+4j+4j+8*-1)/(1+2j-2j-4*-1)
c = (-6+8j)/5
c = -1.2+1.6j

পাইথন কনসোল সেশন অনুসরণ করে উপরের চিকিত্সা যাচাই করে।

>>> a = 2+4j
>>> b = 1-2j
>>> a/b
(-1.2+1.6j)

cmath মডিউল

পাইথনের স্ট্যান্ডার্ড লাইব্রেরি প্রক্রিয়া ফ্লোটিং পয়েন্ট সংখ্যার গণিত মডিউলে সংজ্ঞায়িত গাণিতিক ফাংশন। জটিল সংখ্যার জন্য, পাইথন লাইব্রেরিতে cmath মডিউল রয়েছে।

জটিল সংখ্যা z =x+yj একটি কার্টেসিয়ান উপস্থাপনা। এটি অভ্যন্তরীণভাবে তার মডুলাস r (যেমন বিল্ট-ইন abs() ফাংশন দ্বারা প্রত্যাবর্তিত হয়) এবং ফেজ কোণ Φ (ফাই হিসাবে উচ্চারিত) যা রেডিয়ানে ঘড়ির কাঁটার বিপরীত কোণ, x অক্ষ এবং লাইনের মধ্যে x এর সাথে মিলিত হওয়ার মধ্যবর্তীভাবে উপস্থাপন করা হয়। মূল নিম্নোক্ত চিত্রটি জটিল সংখ্যা −

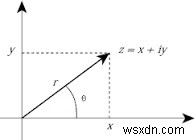
cmath মডিউলের ফাংশনগুলি কার্টেসিয়ান উপস্থাপনাকে পোলার প্রতিনিধিত্বে রূপান্তর করতে দেয় এবং এর বিপরীতে।

পোলার() − এই ফাংশনটি জটিল সংখ্যার কার্টেসিয়ান স্বরলিপির মেরু উপস্থাপনা প্রদান করে। রিটার্ন মান হল একটি টিপল যা মডুলাস এবং ফেজ নিয়ে গঠিত।

>>> import cmath
>>> a = 2+4j
>>> cmath.polar(a)
(4.47213595499958, 1.1071487177940904)

লক্ষ্য করুন যে মডুলাস abs() ফাংশন

>>> abs(a)
4.47213595499958

ফেজ() − এই ফাংশনটি x অক্ষ এবং সেগমেন্ট জয়েনিং a এর মধ্যে ঘড়ির কাঁটার বিপরীত কোণ প্রদান করে উৎপত্তি সহ। কোণটি রেডিয়ানে উপস্থাপিত হয় এবং এটি π এবং -π

>>> cmath.phase(a)
1.1071487177940904
z = x+yj
Φ

rect() − এই ফাংশনটি পোলার আকারে অর্থাৎ মডুলাস এবং ফেজে প্রতিনিধিত্ব করা জটিল সংখ্যার কার্টেসিয়ান উপস্থাপনা প্রদান করে

>>> cmath.rect(4.47213595499958, 1.1071487177940904)
(2.0000000000000004+4j)

cmath মডিউলটিতে গণিত মডিউলে সংজ্ঞায়িত সমস্ত গাণিতিক ফাংশনের বিকল্প রয়েছে। নিচে ব্যাখ্যা করা হয়েছে −

cmath.sin() − এই ফাংশন রেডিয়ানে উপস্থাপিত ফেজ কোণের সাইন ত্রিকোণমিতিক অনুপাত প্রদান করে৷

>>> import cmath
>>> a = 2+4j
>>> p = cmath.phase(a)
>>> cmath.sin(p)
(0.8944271909999159+0j)

একইভাবে, অন্যান্য অনুপাতের জন্য ফাংশন cos(), tan(), asin(), acos() এবং atan() cmath মডিউলে সংজ্ঞায়িত করা হয়েছে।

cmath.exp() − math.exp(এর মতো), এই ফাংশনটি ex ফেরত দেয় যেখানে x একটি জটিল সংখ্যা এবং e হল 2.71828

>>> cmath.exp(a)
(-1.1312043837568135+2.4717266720048188j)

cmath.log10() − এই ফাংশনটি 10

>>> a = 1+2j
>>> cmath.log10(a)
(0.3494850021680094+0.480828578784234j)

cmath.sqrt() − এই ফাংশনটি জটিল সংখ্যার বর্গমূল প্রদান করে।

>>> cmath.sqrt(a)
(1.272019649514069+0.7861513777574233j)

এই নিবন্ধে আমরা পাইথনের জটিল সংখ্যা ডেটা টাইপের গুরুত্বপূর্ণ বৈশিষ্ট্য এবং কীভাবে এটিতে গাণিতিক ক্রিয়াকলাপ করা যায় তা শিখেছি। আমরা cmath মডিউলে সংজ্ঞায়িত বিভিন্ন ফাংশনও অন্বেষণ করেছি।