পাইথনে সমস্ত চালান সম্পূর্ণ করার জন্য মোট খরচ খোঁজার প্রোগ্রাম

ধরুন আমাদের কাছে পোর্ট নামক তালিকার একটি তালিকা আছে, যেখানে পোর্ট[i] সেই পোর্টের তালিকাকে প্রতিনিধিত্ব করে যে পোর্টের সাথে i সংযুক্ত। আমাদের কাছে শিপমেন্ট নামক তালিকার আরেকটি তালিকা রয়েছে যেখানে সিকোয়েন্সের প্রতিটি তালিকা [i, j] যা বোঝায় যে পোর্ট i থেকে পোর্ট j পর্যন্ত একটি চালানের অনুরোধ রয়েছে। এবং পোর্ট i থেকে পোর্ট j পর্যন্ত জাহাজের খরচ হল দুটি বন্দর থেকে সংক্ষিপ্ততম পথের দৈর্ঘ্য, আমাদের সমস্ত চালান সম্পূর্ণ করার জন্য প্রয়োজনীয় মোট খরচ খুঁজে বের করতে হবে।

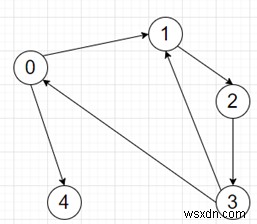
সুতরাং, যদি ইনপুটটি পোর্টের মত হয় =[[1, 4],[2],[3],[0, 1],[]] শিপমেন্ট =[[1, 4]], তাহলে আউটপুট হবে 4, যেহেতু পথটি 1 -> 2 -> 3 -> 0 -> 4 থেকে।

এটি সমাধানের জন্য, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• n :=পোর্টের আকার
• dist :=পোর্ট তালিকা থেকে সংলগ্ন ম্যাট্রিক্স
0 থেকে n রেঞ্জে j-এর জন্য
• করুন
  • আমি 0 থেকে n রেঞ্জের জন্য, কর
    0 থেকে n রেঞ্জে k-এর জন্য
    • করুন
      • dist[i, k] =সর্বনিম্ন dist[i, k], dist[i, j] + dist[j, k]
• যখন dist[i,j] অসীম না হয় তখন [i, j] আকারে সমস্ত চালানের জন্য একটি তালিকা তৈরি করুন।
• উৎপন্ন তালিকার যোগফল ফেরত দিন।

আরও ভালভাবে বোঝার জন্য আসুন নিম্নলিখিত বাস্তবায়ন দেখি:

উদাহরণ

class Solution:
   def solve(self, ports, shipments):
      n = len(ports)
      INF = 10 ** 10
      dist = [[INF for _ in range(n)] for _ in range(n)]
      for i in range(n):
         dist[i][i] = 0
      for i in range(n):
         for j in ports[i]:
            dist[i][j] = 1
      for j in range(n):
         for i in range(n):
            for k in range(n):
               dist[i][k] = min(dist[i][k], dist[i][j] + dist[j][k])

      return sum(dist[i][j] for i, j in shipments if dist[i][j] != INF)

ob = Solution()
ports = [[1, 4],[2],[3],[0, 1],[]]
shipments = [[1, 4]]
print(ob.solve(ports, shipments))

ইনপুট

[[1, 4],[2],[3],[0, 1],[]], [[1, 4]]

আউটপুট

4