পাইথনে ন্যূনতম খরচ সহ শহরগুলিকে সংযুক্ত করা

ধরুন 1 থেকে N পর্যন্ত সংখ্যায় N শহর আছে। আমাদের সংযোগ আছে, যেখানে প্রতিটি সংযোগ [i] হল [city1, city2, cost] এটি city1 এবং city2 কে একসাথে সংযুক্ত করার খরচকে প্রতিনিধিত্ব করে . আমাদের ন্যূনতম খরচ খুঁজে বের করতে হবে যাতে প্রতিটি জোড়া শহরের জন্য, সংযোগের একটি পথ বিদ্যমান থাকে (সম্ভবত দৈর্ঘ্য 1) যা ঐ দুটি শহরকে একসাথে সংযুক্ত করে। খরচ হল সংযোগ খরচের যোগফল। যদি কাজটি অসম্ভব হয় তবে -1 ফেরত দিন।

তাই যদি গ্রাফ −

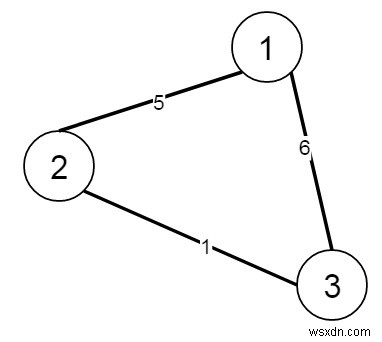
তারপর আউটপুট হবে 6, যেকোনো দুটি শহর বেছে নিলে সমস্ত শহর সংযুক্ত হবে, তাই আমরা ন্যূনতম 2, [1, 5]

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• Find() নামক পদ্ধতি সংজ্ঞায়িত করুন, এটি x

  লাগবে

• যদি অভিভাবক[x] -1 হয়, তাহলে x

  ফেরত দিন

• পিতামাতা[x] :=খুঁজুন(অভিভাবক[x])

• ফেরত অভিভাবক[x]

• ইউনিয়ন() নামে আরেকটি পদ্ধতি তৈরি করুন, এটি x এবং y

  লাগবে

• parent_x :=find(x), parent_y :=find(y)

• যদি parent_x =parent_y, তাহলে ফিরে যান, অন্যথায় parent[parent_y] :=parent_x

• প্রধান পদ্ধতি থেকে, এটি n এবং conn

  লাগবে

• parent :=n আকারের একটি অ্যারে এবং এটি – 1 দিয়ে পূরণ করুন, ডিসজয়েন্ট সেট করুন :=n – 1, খরচ :=0

• c :=conn এর সাজানো তালিকা, খরচের উপর ভিত্তি করে এটি সাজান

• i :=0

• যখন i

  • x :=c[i, 0] এবং y :=c[i, 1]

  • যদি find(x) find(y) এর মতো না হয়, তাহলে 1 দ্বারা বিচ্ছিন্নতা হ্রাস করুন, c[i, 2] দ্বারা ব্যয় বৃদ্ধি করুন এবং মিলন (x, y) সম্পাদন করুন

  • i 1 দ্বারা বাড়ান

• ডিসজয়েন্ট 0 হলে ফেরত খরচ, অন্যথায় ফেরত -1

উদাহরণ(পাইথন)

আরো ভালোভাবে বোঝার জন্য নিচের বাস্তবায়নটি দেখি -

class Solution(object):
   def find(self, x):
      if self.parent[x] == -1:
         return x
      self.parent[x] = self.find(self.parent[x])
      return self.parent[x]
   def union(self,x,y):
      parent_x = self.find(x)
      parent_y = self.find(y)
      if parent_x == parent_y:
         return
      self.parent[parent_y] = parent_x
   def minimumCost(self, n, connections):
      self.parent = [ -1 for i in range(n+1)]
      disjoint = n-1
      cost = 0
      c = sorted(connections,key=lambda v:v[2])
      i = 0
      while i<len(c) and disjoint:
         x = c[i][0]
         y = c[i][1]
         if self.find(x)!=self.find(y):
            disjoint-=1
            cost+=c[i][2]
            self.union(x,y)
            i+=1
         return cost if not disjoint else -1
ob = Solution()
print(ob.minimumCost(3, [[1,2,5], [1,3,6], [2,3,1]]))

ইনপুট

3
[[1,2,5],[1,3,6],[2,3,1]]

আউটপুট

-1