পাইথনে একটি বোর্ডকে বর্গাকারে কাটতে ন্যূনতম খরচ

ধরুন আমাদের দৈর্ঘ্য p এবং প্রস্থ q এর একটি বোর্ড আছে; আমাদের এই বোর্ডটিকে p*q সংখ্যক বর্গক্ষেত্রে ভাঙ্গতে হবে যাতে ভাঙার খরচ যতটা সম্ভব ন্যূনতম হয়। প্রতিটি প্রান্তের জন্য কাটিং খরচ দেওয়া হবে।

সুতরাং, যদি ইনপুট হয় X_slice =[3,2,4,2,5], Y_slice =[5,2,3]

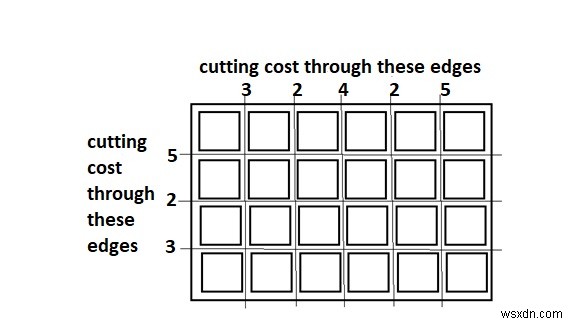
তাহলে আউটপুট হবে 65

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• res :=0
• অনুভূমিক :=1, উল্লম্ব :=1
• i :=0, j :=0
• যখন i
• যদি X_slice[i]> Y_slice[j], তাহলে
  • res :=res + X_slice[i] * উল্লম্ব
  • অনুভূমিক :=অনুভূমিক + 1
  • i :=i + 1
• অন্যথায়,
  • res :=res + Y_slice[j] * অনুভূমিক
  • উল্লম্ব :=উল্লম্ব + 1
  • j :=j + 1

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

def minCost(X_slice, Y_slice, m, n):
   res = 0
   X_slice.sort(reverse = True)
   Y_slice.sort(reverse = True)
   horizontal = 1
   vertical = 1
   i = 0
   j = 0
   while i < m and j < n:
      if (X_slice[i] > Y_slice[j]):
         res += X_slice[i] * vertical
         horizontal += 1
         i += 1
      else:
         res += Y_slice[j] * horizontal
         vertical += 1
         j += 1
   total = 0
   while (i < m):
      total += X_slice[i]
      i += 1
   res += total * vertical
   total = 0
   while (j < n):
      total += Y_slice[j]
      j += 1
   res += total * horizontal
   return res
m = 6; n = 4
X_slice = [3,2,4,2,5]
Y_slice = [5,2,3]
print(minCost(X_slice, Y_slice, m-1, n-1))

ইনপুট

[3,2,4,2,5],[5,2,3]

আউটপুট

65