পাইথনে পাতার মান থেকে ন্যূনতম খরচ গাছ

ধরুন আমাদের কাছে ধনাত্মক পূর্ণসংখ্যার একটি বিন্যাস রয়েছে, সমস্ত বাইনারি গাছ বিবেচনা করুন যেমন −

• প্রতিটি নোডে 0 বা 2টি শিশু থাকে;
• অ্যার অ্যারের মানগুলি গাছের ক্রমানুসারে প্রতিটি পাতার মানগুলির সাথে মিলে যায়৷
• প্রতিটি নন-লিফ নোডের মান যথাক্রমে তার বাম এবং ডান সাবট্রির বৃহত্তম পাতার মানের গুণফলের সমান৷

বিবেচনা করা সমস্ত সম্ভাব্য বাইনারি গাছের মধ্যে, আমাদের প্রতিটি নন-লিফ নোডের মানের সম্ভাব্য ক্ষুদ্রতম যোগফল খুঁজে বের করতে হবে। সুতরাং যদি ইনপুট arr হয় [6,2,4], তাহলে আউটপুট হবে 32, কারণ সেখানে সম্ভবত দুটি গাছ থাকতে পারে −

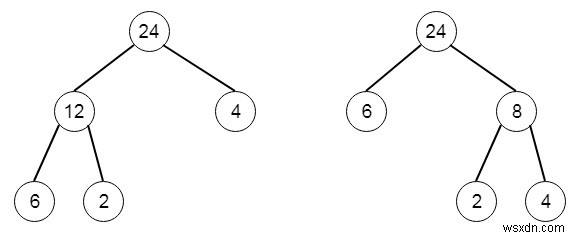
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• মেমো নামে একটি মানচিত্র তৈরি করুন
• একটি পদ্ধতি dp() সংজ্ঞায়িত করুন, এটি পরামিতি হিসাবে i এবং j গ্রহণ করবে। এটি নিম্নরূপ কাজ করবে -
• যদি j <=i, তাহলে 0 ফেরত দিন
• যদি মেমোতে (i, j) থাকে, তাহলে মেমো ফেরত দিন[(i, j)]
• res :=অসীম
• k এর জন্য i থেকে j – 1
  পরিসরে
  • res :=res এর সর্বনিম্ন, dp(i, k) + dp(k + 1, j) + (index i থেকে k + 1 পর্যন্ত অ্যারের সাবয়ারের সর্বোচ্চ) * k + 1 থেকে অ্যারের সাবয়ারের সর্বোচ্চ j + 1
  থেকে
• মেমো[(i, j)] :=res
• রিটার্ন মেমো[(i, j)]
• প্রধান পদ্ধতিটি এই dp() পদ্ধতিটিকে − call dp(0, arr-এর দৈর্ঘ্য - 1) হিসাবে কল করবে

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

উদাহরণ

class Solution(object):
   def mctFromLeafValues(self, arr):
      """
      :type arr: List[int]
      :rtype: int
      """
      self. memo = {}
      def dp(i,j):
         if j<=i:
            return 0
         if (i,j) in self.memo:
            return self.memo[(i,j)]
         res = float('inf')
         for k in range(i,j):
            res = min(res,dp(i,k) + dp(k+1,j) + (max(arr[i:k+1])*max(arr[k+1:j+1])))
         self.memo[(i,j)]=res
         return self.memo[(i,j)]
      return dp(0,len(arr)-1)

ইনপুট

[6,2,4]

আউটপুট

32