পাইথনে n x m আকারের আয়তক্ষেত্রের ভিতরে 2x1 আকারের আয়তক্ষেত্রের সংখ্যা খুঁজুন

ধরুন আমাদের দুটি মান আছে n এবং m; আমাদের 2x1 আকারের আয়তক্ষেত্রের সংখ্যা খুঁজে বের করতে হবে যা n x m আকারের আয়তক্ষেত্রের ভিতরে সেট করা যেতে পারে। কিছু শর্ত আছে, যা আমাদের বিবেচনা করতে হবে -

যেকোনো দুটি ছোট আয়তক্ষেত্র ওভারল্যাপ করতে পারে না।
প্রতিটি ছোট আয়তক্ষেত্র সম্পূর্ণভাবে বড়টির ভিতরে থাকে। এটি বড় আয়তক্ষেত্রের প্রান্ত স্পর্শ করার অনুমতি দেওয়া হয়।

সুতরাং, যদি ইনপুট মত হয়

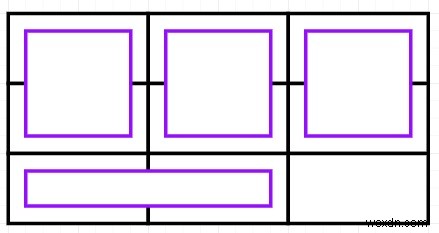
n =3, m =3, তাহলে আউটপুট হবে 4

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

যদি n mod 2 0 এর মত হয়, তাহলে
- ফেরত (n / 2) * m
অন্যথায় যখন m mod 2 0 হয়, তখন
- রিটার্ন (m / 2) * n
রিটার্ন (n * m - 1) / 2

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

def count_rect(n, m):
   if (n % 2 == 0):
      return (n / 2) * m
   elif (m % 2 == 0):
      return (m // 2) * n
   return (n * m - 1) // 2
n = 3
m = 3
print(count_rect(n, m))

ইনপুট:

3, 3