পাইথনের একটি গাছে ঠিক k এর দূরত্ব রয়েছে এমন স্বতন্ত্র জোড়া শীর্ষবিন্দুর সংখ্যা খুঁজুন

ধরুন আমাদের একটি পূর্ণসংখ্যা k আছে এবং n নোড সহ একটি ট্রিও আছে, আমাদেরকে সঠিক k দূরত্বের শীর্ষবিন্দুর স্বতন্ত্র জোড়ার সংখ্যা গণনা করতে হবে৷

সুতরাং, যদি ইনপুট k =2

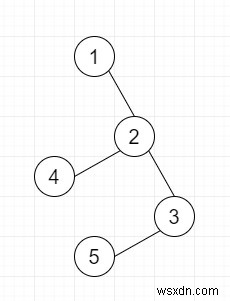
তাহলে আউটপুট হবে 4

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• N :=5005

• গ্রাফ :=আকারের সংলগ্ন তালিকা N

• vertex_count :=505 x 5005 আকারের একটি 2d ​​ম্যাট্রিক্স

• res :=0

• একটি ফাংশন সংজ্ঞায়িত করুন insert_edge()। এটি x, y

  লাগবে

  • গ্রাফের শেষে y সন্নিবেশ করান[x]

  • গ্রাফ[y]

    এর শেষে x সন্নিবেশ করুন

• একটি ফাংশন dfs() সংজ্ঞায়িত করুন। এটি v, parent

  লাগবে

• vertex_count[v, 0] :=1

• প্রতিটি i জন্য গ্রাফ[v], do

  • আমি যদি অভিভাবক হিসাবে একই না হই, তাহলে

    • dfs(i, v)

    • 1 থেকে k + 1 রেঞ্জে j এর জন্য, করুন

      • res :=res + vertex_count[i, j - 1] * vertex_count[v, k - j]

    • 1 থেকে k + 1 রেঞ্জে j এর জন্য, করুন

      • vertex_count[v, j] :=vertex_count[v, j] + vertex_count[i, j - 1]

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

N = 5005
graph = [[] for i in range(N)]
vertex_count = [[0 for i in range(505)] for i in range(N)]
res = 0
def insert_edge(x, y):
   graph[x].append(y)
   graph[y].append(x)
def dfs(v, parent):
   global res
   vertex_count[v][0] = 1
   for i in graph[v]:
      if (i != parent):
         dfs(i, v)
         for j in range(1, k + 1):
            res += vertex_count[i][j - 1] * vertex_count[v][k - j]
         for j in range(1, k + 1):
            vertex_count[v][j] += vertex_count[i][j - 1]
k = 2
insert_edge(1, 2)
insert_edge(2, 3)
insert_edge(3, 4)
insert_edge(2, 5)
dfs(1, 0)
print(res)

ইনপুট

k = 2
insert_edge(1, 2)
insert_edge(2, 3)
insert_edge(3, 4)
insert_edge(2, 5)

আউটপুট

4