ধরুন আমাদের কাছে একটি নির্দেশিত অ্যাসাইক্লিক গ্রাফ আছে যা সংলগ্ন তালিকা দ্বারা উপস্থাপিত হয়। আমাদের নোড পুনরাবৃত্তি ছাড়াই গ্রাফে দীর্ঘতম পথ খুঁজে বের করতে হবে।
সুতরাং, যদি ইনপুট মত হয়
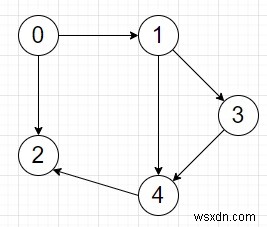
তাহলে আউটপুট হবে 4, কারণ পথটি 0 -> 1 -> 3 -> 4 -> 2 এর দৈর্ঘ্য 4।
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
- উত্তর :=0
- n :=গ্রাফের নোড গণনা
- টেবিল :=n আকারের একটি তালিকা এবং -1 দিয়ে পূরণ করুন
- একটি ফাংশন dfs() সংজ্ঞায়িত করুন। এটি আপনাকে নিয়ে যাবে
- যদি টেবিল[u] -1 না হয়, তাহলে
- রিটার্ন টেবিল[u]
- p_len :=0
- গ্রাফ[u]-এ প্রতিটি vectex v-এর জন্য
- করুন
- p_len :=সর্বোচ্চ p_len এবং (1 + dfs(v))
- টেবিল[u] :=p_len
- p_len ফেরত দিন
- প্রধান পদ্ধতি থেকে নিম্নলিখিতগুলি করুন -
- আমি 0 থেকে n রেঞ্জের জন্য, কর
- উত্তর :=সর্বাধিক উত্তর, dfs(i)
- উত্তর ফেরত দিন
উদাহরণ (পাইথন)
আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -
class Solution: def solve(self, graph): ans = 0 n = len(graph) table = [-1] * n def dfs(u): if table[u] != -1: return table[u] p_len = 0 for v in graph[u]: p_len = max(p_len, 1 + dfs(v)) table[u] = p_len return p_len for i in range(n): ans = max(ans, dfs(i)) return ans ob = Solution() graph = [ [1, 2], [3, 4], [], [4], [2], ] print(ob.solve(graph))ফেরত দিন
ইনপুট
graph = [[1, 2],[3, 4],[],[4],[2]]
আউটপুট
4


