পাইথনে একটি বাইনারি গাছের দীর্ঘতম ধারাবাহিক পথের দৈর্ঘ্য খুঁজে বের করার প্রোগ্রাম

ধরুন আমাদের একটি বাইনারি গাছ আছে; আমাদের বাইনারি ট্রিতে দীর্ঘতম পথ খুঁজে বের করতে হবে।

সুতরাং, যদি ইনপুট মত হয়

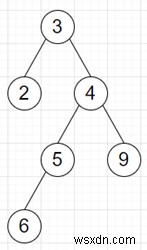
তাহলে আউটপুট হবে 5 কারণ দীর্ঘতম ধারাবাহিক ক্রম হল [2, 3, 4, 5, 6]।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• যদি রুট নাল হয়, তাহলে
  • রিটার্ন 0
• maxPath :=0
• একটি ফাংশন সাহায্যকারী() সংজ্ঞায়িত করুন। এটি নোড গ্রহণ করবে
• inc :=1, dec :=1
• নোডের বাম অংশ যদি শূন্য না হয়, তাহলে
  • [left_inc, left_dec] :=সাহায্যকারী(নোডের বাম)
• অন্যথায়,
  • [left_inc, left_dec] :=[0, 0]
• যদি নোডের ডানদিকে শূন্য না হয়, তাহলে
  • [right_inc, right_dec] :=সাহায্যকারী(নোডের ডানদিকে)
• অন্যথায়,
  • [right_inc, right_dec] :=[0, 0]
• যদি নোডের বাম অংশটি শূন্য না হয় এবং নোডের মান - নোডের বাঁদিকের মান 1 এর মত হয়, তাহলে
  • inc :=সর্বোচ্চ inc এবং (left_inc + 1)
• অন্যথায় যখন নোডের বাম অংশ নাল না হয় এবং নোডের মান - নোডের বামদিকের মান -1 এর মত হয়, তাহলে
  • ডিসে :=সর্বোচ্চ ডিসেম্বর এবং (বাম_ডিসে + 1)
• যদি নোডের রাইট নাল না হয় এবং নোডের মান - নোডের ডানের মান 1 এর মত হয়, তাহলে
  • inc :=সর্বোচ্চ inc এবং (right_inc + 1)
• অন্যথায় যখন নোডের রাইট নাল না হয় এবং নোডের মান - নোডের ডানের মান -1 এর মত হয়, তাহলে
  • dec :=সর্বোচ্চ ডিসেম্বর এবং (right_dec + 1)
• যদি নোডের বাম অংশ নাল না হয় এবং নোডের ডানদিকে নাল না হয় এবং নোডের বাঁদিকের মান নাল না হয় - নোডের মান 1 এবং নোডের মান - নোডের ডানের মান 1 এর মতো, তাহলে
  • maxPath :=সর্বাধিক maxPath এবং (left_dec + right_inc + 1)
• অন্যথায় যখন নোড নোডের বাম অংশ নাল না হয় এবং নোডের ডানদিকে নাল না হয় এবং নোডের বাম মান নাল না হয় - নোডের মান -1 এর মত হয়, তারপর
  • maxPath :=সর্বাধিক maxPath এবং (left_inc + right_dec + 1)
• maxPath :=maxPath, inc এবং dec-এর সর্বাধিক
• রিটার্ন ইনক, ডিসেম্বর
• প্রধান পদ্ধতি থেকে নিম্নলিখিতগুলি করুন:
• সহায়ক(রুট)
• maxPath ফেরত দিন

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

উদাহরণ

class TreeNode:
   def __init__(self, data, left = None, right = None):
      self.val = data
      self.left = left
      self.right = right
     
def print_tree(root):
   if root is not None:
      print_tree(root.left)
      print(root.val, end = ', ')
      print_tree(root.right)

class Solution:
   def solve(self, root):
      if not root:
         return 0
      self.maxPath = 0

      def helper(node):
         inc, dec = 1, 1
         if node.left:
            left_inc, left_dec = helper(node.left)
         else:
            left_inc, left_dec = 0, 0
         if node.right:
            right_inc, right_dec = helper(node.right)
         else:
            right_inc, right_dec = 0, 0

         if node.left and node.val - node.left.val == 1:
            inc = max(inc, left_inc + 1)
         elif node.left and node.val - node.left.val == -1:
            dec = max(dec, left_dec + 1)

         if node.right and node.val - node.right.val == 1:
            inc = max(inc, right_inc + 1)
         elif node.right and node.val - node.right.val == -1:
            dec = max(dec, right_dec + 1)

         if (node.left and node.right and node.left.val - node.val == 1 and node.val - node.right.val == 1):
            self.maxPath = max(self.maxPath, left_dec + right_inc + 1)
         elif (node.left and node.right and node.left.val - node.val == -1
            and node.val - node.right.val == -1):
            self.maxPath = max(self.maxPath, left_inc + right_dec + 1)
           
         self.maxPath = max(self.maxPath, inc, dec)
         return inc, dec

      helper(root)
      return self.maxPath
     
ob = Solution()
root = TreeNode(3)
root.left = TreeNode(2)
root.right = TreeNode(4)
root.right.left = TreeNode(5)
root.right.right = TreeNode(9)
root.right.left.left = TreeNode(6)
print(ob.solve(root))

ইনপুট

root = TreeNode(3)
root.left = TreeNode(2)
root.right = TreeNode(4)
root.right.left = TreeNode(5)
root.right.right = TreeNode(9)
root.right.left.left = TreeNode(6)

আউটপুট

5