ধরুন আমাদের নিচের মত একটি গ্রাফ আছে। সেই গ্রাফটি হল পিটারসন গ্রাফ। শীর্ষবিন্দুগুলি 0 থেকে 9 পর্যন্ত সংখ্যাযুক্ত। প্রতিটি শীর্ষে কিছু অক্ষর রয়েছে। সেই গ্রাফে একটি ওয়াক ওয়াক বিবেচনা করা যাক, যেখানে L শীর্ষবিন্দু ব্যবহার করা হয়েছে। L অক্ষর সহ একটি স্ট্রিং S ওয়াক দ্বারা উপলব্ধি করা হয় যখন W এবং S বর্ণের ক্রম একই হয়। আমরা একাধিকবার শীর্ষবিন্দু পরিদর্শন করতে পারি।
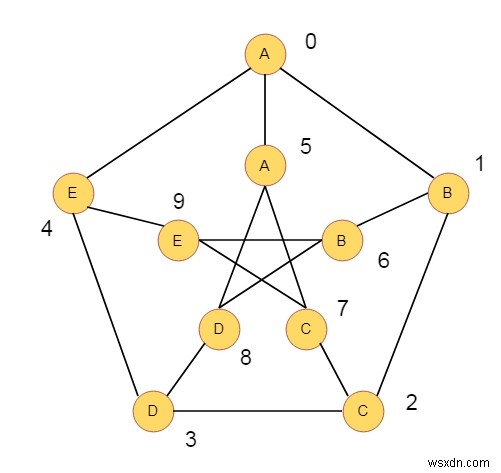
উদাহরণস্বরূপ, একটি স্ট্রিং S "ABBECCD" এর মতো, এটি হাঁটার মাধ্যমে উপলব্ধি করা যায় (0, 1, 6, 9, 7, 2, 3)। আমাদের কাজ হল এই ধরনের হাঁটা খুঁজে বের করা, এবং সেই হাঁটা যদি উপস্থিত থাকে, তাহলে অভিধানের দিক থেকে এমন হাঁটা খুঁজে বের করা। যদি কোন চুষে হাঁটা না থাকে, তাহলে ফিরুন -1।
অ্যালগরিদম
petersonGraphWalk(S, v) −
begin res := starting vertex for each character c in S except the first one, do if there is an edge between v and c in outer graph, then v := c else if there is an edge between v and c+5 in inner graph, then v := c + 5 else return false end if put v into res done return true end
উদাহরণ
#include<iostream>
using namespace std;
bool adj_mat[10][10] = {{0, 1, 0, 0, 1, 1, 0, 0, 0, 0},
{1, 0, 1, 0, 0, 0, 1, 0, 0, 0},
{0, 1, 0, 1, 0, 0, 0, 1, 0, 0},
{0, 0, 1, 0, 1, 0, 0, 0, 1, 0},
{1, 0, 0, 1, 0, 0, 0, 0, 0, 1},
{1, 0, 0, 0, 0, 0, 0, 1, 1, 0},
{0, 1, 0, 0, 0, 0, 0, 0, 1, 1},
{0, 0, 1, 0, 0, 1, 0, 0, 0, 1},
{0, 0, 0, 1, 0, 1, 1, 0, 0, 0},
{0, 0, 0, 0, 1, 0, 1, 1, 0, 0}
};
char S[100005];
char res[100005];
bool petersonGraphWalk(char* S, int v){
res[0] = v + '0';
for(int i = 1; S[i]; i++){
//traverse the outer graph
if(adj_mat[v][S[i] - 'A'] || adj_mat[S[i] - 'A'][v]){
v = S[i] - 'A';
}
//then check the inner graph
else if(adj_mat[v][S[i] - 'A' + 5] || adj_mat[S[i] - 'A' + 5][v]){
v = S[i] - 'A' + 5;
}else{
return false;
}
res[i] = v + '0';
}
return true;
}
main() {
char* str = "ABBECCD";
if(petersonGraphWalk(str, str[0] - 'A') || petersonGraphWalk(str, str[0] - 'A' + 5)){
cout << res;
}else{
cout << -1;
}
} আউটপুট
0169723


