0-1 ন্যাপস্যাক সমস্যার জন্য পাইথন প্রোগ্রাম

এই নিবন্ধে, আমরা নীচে দেওয়া সমস্যার বিবৃতিটির সমাধান সম্পর্কে শিখব৷

সমস্যা বিবৃতি − আমাদেরকে n আইটেমগুলির ওজন এবং মান দেওয়া হয়েছে, আমাদের এই আইটেমগুলিকে W ধারণক্ষমতার ব্যাগে রাখতে হবে সর্বোচ্চ ক্ষমতা w পর্যন্ত। আমাদের সর্বোচ্চ সংখ্যক আইটেম বহন করতে হবে এবং এর মূল্য ফেরত দিতে হবে।

এখন নিচের বাস্তবায়নে সমাধানটি পর্যবেক্ষণ করা যাক -

# ব্রুট-ফোর্স অ্যাপ্রোচ

উদাহরণ

#Returns the maximum value that can be stored by the bag
def knapSack(W, wt, val, n):
   # initial conditions
   if n == 0 or W == 0 :
      return 0
   # If weight is higher than capacity then it is not included
   if (wt[n-1] > W):
      return knapSack(W, wt, val, n-1)
   # return either nth item being included or not
   else:
      return max(val[n-1] + knapSack(W-wt[n-1], wt, val, n-1),
         knapSack(W, wt, val, n-1))
# To test above function
val = [50,100,150,200]
wt = [8,16,32,40]
W = 64
n = len(val)
print (knapSack(W, wt, val, n))

আউটপুট

350

#গতিশীল পদ্ধতি

উদাহরণ

# a dynamic approach
# Returns the maximum value that can be stored by the bag
def knapSack(W, wt, val, n):
   K = [[0 for x in range(W + 1)] for x in range(n + 1)]
   #Table in bottom up manner
   for i in range(n + 1):
      for w in range(W + 1):
         if i == 0 or w == 0:
            K[i][w] = 0
         elif wt[i-1] <= w:
            K[i][w] = max(val[i-1] + K[i-1][w-wt[i-1]], K[i-1][w])
         else:
            K[i][w] = K[i-1][w]
   return K[n][W]
#Main
val = [50,100,150,200]
wt = [8,16,32,40]
W = 64
n = len(val)
print(knapSack(W, wt, val, n))

আউটপুট

350

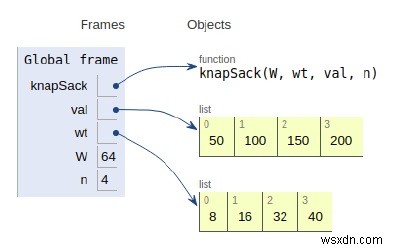
সমস্ত ভেরিয়েবল স্থানীয় সুযোগে ঘোষণা করা হয়েছে এবং তাদের উল্লেখ উপরের চিত্রে দেখা যাচ্ছে।

উপসংহার

এই নিবন্ধে, আমরা শিখেছি কিভাবে আমরা 0-1 Knapsack সমস্যার জন্য একটি পাইথন প্রোগ্রাম তৈরি করতে পারি