রুবিতে ব্যবহারিক গ্রাফ তত্ত্ব

এটি "ব্যবহারিক কম্পিউটার বিজ্ঞান" সিরিজের পরবর্তী কিস্তি, যেখানে আপনি রুবি ব্যবহার করে বাস্তব সমস্যা সমাধানের জন্য ক্লাসিক কম্পিউটার বিজ্ঞান ধারণাগুলি কীভাবে প্রয়োগ করবেন তা শিখবেন৷

আজ আমরা গ্রাফ থিওরি সম্পর্কে কথা বলতে যাচ্ছি .

আপনি বাইনারি গাছ সম্পর্কে শুনে থাকতে পারেন, তারা দেখতে এইরকম:

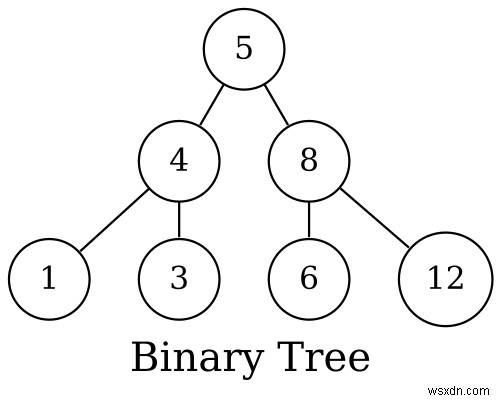
ব্যাপারটি হল একটি বাইনারি গাছ একটি গ্রাফের একটি বিশেষ সংস্করণ, যাতে এটি আপনাকে গ্রাফগুলি কতটা বিস্তৃত তা সম্পর্কে ধারণা দেয়৷

চলুন শুরু করা যাক গ্রাফ থিওরি ফান্ডামেন্টালগুলির একটি ওভারভিউ দিয়ে, তারপর আমরা দেখতে যাচ্ছি কিছু ব্যবহারিক ব্যবহার কী এবং কীভাবে এটি রুবিতে প্রয়োগ করা যায়!

গ্রাফের মৌলিক বিষয়গুলি

একটি গ্রাফ দুটি উপাদানের সমন্বয়ে গঠিত:

• নোড (বা শীর্ষবিন্দু)
• প্রান্তগুলি

একটি নোড গ্রাফের একটি উপাদানকে প্রতিনিধিত্ব করে, যেমন একটি শহর বা একটি রাস্তা, একটি মানচিত্রের প্রতিনিধিত্বকারী একটি গ্রাফে। যখন প্রান্তগুলি নোডগুলির মধ্যে সংযোগগুলিকে উপস্থাপন করে৷

আপনি যদি একটি কম্পিউটার বিজ্ঞান বা গণিত বইটি দেখেন তবে আপনি এই সূত্র দ্বারা সংজ্ঞায়িত একটি গ্রাফ দেখতে পাবেন:G(V, E) .

যেখানে G মানে গ্রাফ, V শীর্ষবিন্দু এবং E এর সেট প্রান্তের সেট।

গ্রাফগুলি নির্দেশিত বা অনির্দেশিত হতে পারে। এর মানে হল যে আপনি শুধুমাত্র একটি দিক (নির্দেশিত গ্রাফ) বা উভয় দিক (অনির্দেশিত গ্রাফ) যেতে পারেন।

গ্রাফের সবচেয়ে জনপ্রিয় ধরন হল নির্দেশিত অ্যাসাইক্লিক গ্রাফ (ডিএজি)। অ্যাসাইক্লিক মানে হল কোন লুপ নেই, ব্যাকট্র্যাক করার কোন উপায় নেই।

গ্রাফের জন্য ব্যবহার করা হয়

এখন যেহেতু আমরা মৌলিক বিষয়গুলির একটি ওভারভিউ দেখেছি, আসুন গ্রাফের কিছু সাধারণ ব্যবহার দেখি৷

গ্রাফ ব্যবহার করে আপনি কিছু করতে পারেন যেমন:

• দুটি অবস্থানের মধ্যে সবচেয়ে ছোট (বা দীর্ঘতম) পথটি খুঁজুন
• দুটি জিনিস একে অপরের সাথে সম্পর্কিত কিনা তা পরীক্ষা করুন
• একটি সুপারিশ ইঞ্জিন তৈরি করুন
• নির্ভরতা বিশ্লেষণ করুন

আরেকটি উদাহরণের মধ্যে রয়েছে একটি গন্তব্যে যাওয়ার সর্বোত্তম রুট খোঁজা (মনে করুন GPS ডিভাইসগুলি)।

কীভাবে গ্রাফ বাস্তবায়ন ও ব্যবহার করবেন

আপনি আপনার নিজস্ব গ্রাফ বাস্তবায়ন লিখতে পারেন, কিন্তু এই নিবন্ধটির জন্য আমরা RGL রত্নকে আটকে রাখব যা ইতিমধ্যেই আমাদের জন্য একটি প্রয়োগ করেছে৷

RGL ব্যবহার করে একটি মৌলিক গ্রাফ তৈরি করতে:

require 'rgl/adjacency'

graph = RGL::DirectedAdjacencyGraph.new

graph.add_edge 1,2
graph.add_edge 3,4
graph.add_edge 1,4
graph.add_edge 4,3

এই কোডটি নিম্নলিখিত গ্রাফ তৈরি করে:

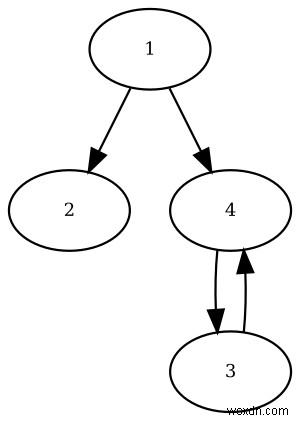
আপনি এইভাবে আপনার গ্রাফের একটি গ্রাফিক্যাল উপস্থাপনা পেতে পারেন:

require 'rgl/dot'

graph.print_dotted_on

তারপরে সেই পদ্ধতির আউটপুটটি একটি সাইটে অনুলিপি করুন যা ডট ভাষা প্রক্রিয়া করতে পারে। এটি পছন্দ করুন।

বিকল্পভাবে, স্থানীয়ভাবে ছবি তৈরি করতে আপনি আপনার মেশিনে Graphviz ইনস্টল করতে পারেন।

এখন যেহেতু আমাদের কাছে একটি গ্রাফ আছে, আমরা এটি সম্পর্কে তথ্য জানার জন্য এটি অতিক্রম করতে চাই।

আপনার গ্রাফ অনুসন্ধানের জন্য দুটি মৌলিক অ্যালগরিদম আছে :

• ব্রেডথ-ফার্স্ট সার্চ (BFS)
• গভীর-প্রথম অনুসন্ধান (DFS)

BFS-এ আপনি প্রথমে সবচেয়ে কাছের নোডগুলি পান এবং DFS-এ আপনি প্রতিটি নোডের জন্য যতটা সম্ভব গভীরে যান। এই অ্যালগরিদমগুলি স্ট্যাক ডেটা স্ট্রাকচার ব্যবহার করে প্রয়োগ করা যেতে পারে।

RGL রত্নটি ইতিমধ্যেই আপনার জন্য সেই অ্যালগরিদমগুলি প্রয়োগ করে:

require 'rgl/traversal'

graph.bfs_iterator.to_a
# [1, 2, 4, 3]

graph.dfs_iterator.to_a
# [1, 4, 3, 2]

গ্রাফটি আবার দেখুন এবং এই অ্যালগরিদমগুলি শুধুমাত্র আপনার চোখ ব্যবহার করে যে পথটি অনুসরণ করেছে (অথবা আপনি চাইলে একটি আঙুলও ব্যবহার করতে পারেন)। এটি আপনাকে কী ঘটছে তা বুঝতে সাহায্য করবে।

ভারিত গ্রাফ

আমরা একটি গ্রাফে ওজনের আকারে আরও তথ্য যোগ করতে পারি যাতে এটি আরও উপযোগী হয়।

ওজনগুলি প্রান্তগুলিতে দেওয়া হয়, যা দুটি নোডের মধ্যে পথ ("শীর্ষ" নামেও পরিচিত)। এই ওজনগুলি এক বিন্দু থেকে অন্য বিন্দুতে যাওয়ার খরচের প্রতিনিধিত্ব করে৷

উদাহরণস্বরূপ, যদি আমাদের কাছে একটি গ্রাফ আকারে একটি দেশের মানচিত্র থাকে এবং আমরা একটি নির্দিষ্ট গন্তব্যে সবচেয়ে কম সময়ে পৌঁছাতে চাই, তাহলে ওজন দুটি শহরের মধ্যে দূরত্বকে প্রতিনিধিত্ব করবে।

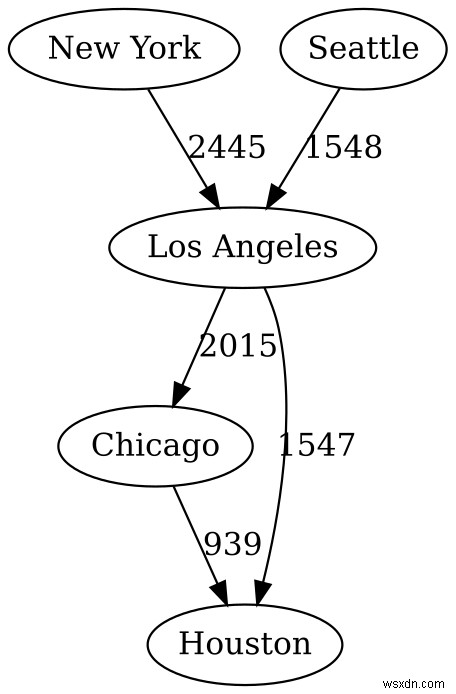
অথবা যদি আমাদের একটি কম্পিউটার নেটওয়ার্ক থাকে, তবে ওজনগুলি একটি নির্দিষ্ট নেটওয়ার্কে পৌঁছাতে কতগুলি হপস লাগে তা বোঝাতে পারে৷

"কম্পিউটার নেটওয়ার্কিংয়ে, একটি হপ হল উৎস এবং গন্তব্যের মধ্যে পথের একটি অংশ। ডেটা প্যাকেটগুলি ব্রিজ, রাউটার এবং গেটওয়ের মধ্য দিয়ে যায় যখন তারা উত্স এবং গন্তব্যের মধ্যে ভ্রমণ করে। প্রতিবার প্যাকেটগুলি পরবর্তী নেটওয়ার্ক ডিভাইসে প্রেরণ করা হলে, একটি হপ ঘটে।" – উইকিপিডিয়া

এখানে একটি ওজনযুক্ত গ্রাফের জন্য একটি কোড উদাহরণ রয়েছে:

graph = RGL::DirectedAdjacencyGraph.new
graph.add_vertices "Los Angeles", "New York", "Chicago", "Houston", "Seattle"

edge_weights =
{
  ["New York", "Los Angeles"] => 2445,
  ["Los Angeles", "Chicago"] => 2015,
  ["Los Angeles", "Houston"] => 1547,
  ["Chicago", "Houston"] => 939,
  ["Seattle", "Los Angeles"] => 1548
}

edge_weights.each { |(city1, city2), w| graph.add_edge(city1, city2) }

আমরা এখন এক বিন্দু থেকে অন্য বিন্দুতে সবচেয়ে ছোট পথটি অনুসন্ধান করতে পারি। এবং এটি ঠিক পরবর্তী বিভাগের বিষয়!

ছোটতম পথ খোঁজা

একটি গ্রাফের মধ্যে সবচেয়ে ছোট পথ খুঁজে বের করার জন্য একটি জনপ্রিয় অ্যালগরিদম হল "Dijkstra's Shortest Path" অ্যালগরিদম৷

একটি ওজনযুক্ত গ্রাফ দেওয়া, আমরা এই প্রশ্নটি সমাধান করতে Dijkstra এর অ্যালগরিদম ব্যবহার করতে পারি:

"বিন্দু A থেকে বি পয়েন্টে যাওয়ার দ্রুততম উপায় কী?"৷

এখানে একটি কোড উদাহরণ, RGL রত্ন ব্যবহার করে:

p graph.dijkstra_shortest_path(edge_weights, "New York", "Houston")
# ["New York", "Los Angeles", "Houston"]

গ্রাফে উপলব্ধ তথ্য ব্যবহার করে এটি আমাদের নিউ ইয়র্ক থেকে হিউস্টন পর্যন্ত সংক্ষিপ্ততম পথ বলে।

সারাংশ

আপনি শিখেছেন একটি গ্রাফ ডেটা স্ট্রাকচার কী এবং কীভাবে এটি RGL রত্ন দিয়ে ব্যবহার করতে হয়।

আপনি গ্রাফের সাথে কাজ করার জন্য সাধারণ অ্যালগরিদমগুলিও শিখেছেন, যেমন DFS, BFS এবং Dijkstra's৷

এই পোস্টটি শেয়ার করতে ভুলবেন না যদি আপনি এটিকে উপযোগী বলে মনে করেন যাতে আরও বেশি মানুষ এটি উপভোগ করতে পারে 🙂