মেমোরাইজেশন হল ডায়নামিক প্রোগ্রামিং এর উপর ভিত্তি করে একটি কৌশল যা একটি রিকারসিভ অ্যালগরিদমের কর্মক্ষমতা উন্নত করতে ব্যবহার করা হয় যাতে প্রদত্ত ইনপুটগুলির ফলাফলের রেকর্ড রেখে পদ্ধতিটি একই সেট ইনপুটের জন্য একাধিকবার না চলে তা নিশ্চিত করে একটি অ্যারে)। পুনরাবৃত্ত পদ্ধতির টপ-ডাউন পদ্ধতি প্রয়োগ করে মুখস্থ করা সম্ভব।
আসুন আমরা মৌলিক ফিবোনাচি উদাহরণের সাহায্যে এই দৃশ্যটি বুঝতে পারি
1-D স্মৃতিচারণ
আমরা শুধুমাত্র একটি অ ধ্রুবক প্যারামিটার সহ একটি পুনরাবৃত্ত অ্যালগরিদম বিবেচনা করব (শুধুমাত্র একটি প্যারামিটার তার মান পরিবর্তন করে) তাই এই পদ্ধতিটিকে 1-ডি মেমোরাইজেশন বলা হয়। ফিবোনাচি সিরিজে N’th (N পর্যন্ত সমস্ত পদ) খুঁজে বের করার জন্য নিম্নলিখিত কোড।
উদাহরণ
public int fibonacci(int n) {
if (n == 0)
return 0;
if (n == 1)
return 1;
System.out.println("Calculating fibonacci number for: " + n);
return (fibonacci(n - 1) + fibonacci(n - 2));
} আউটপুট
যদি আমরা উপরের কোডটি n=5 দিয়ে চালাই, তাহলে এটি নিম্নলিখিত আউটপুট তৈরি করবে।
Calculating fibonacci number for: 5 Calculating fibonacci number for: 4 Calculating fibonacci number for: 3 Calculating fibonacci number for: 2 Calculating fibonacci number for: 2 Calculating fibonacci number for: 3 Calculating fibonacci number for: 2
n=5:5
এর জন্য ফিবোনাচি মানএটি লক্ষ্য করা যায় যে 2 এবং 3 এর জন্য ফিবোনাচি সংখ্যা একাধিকবার গণনা করা হয়েছে৷ আসুন আমরা উপরের শর্তের ফিবোনাচি সিরিজের জন্য একটি পুনরাবৃত্ত ট্রি আঁকার মাধ্যমে আরও ভালভাবে বুঝতে পারি, যেমন n=5৷
এখানে নোডের দুটি শিশু এটির পুনরাবৃত্তিমূলক কলটি উপস্থাপন করবে। যেমনটি দেখা যায় F(3) এবং F(2) একাধিকবার গণনা করা হয় এবং প্রতিটি ধাপের পরে ফলাফল ক্যাশ করার মাধ্যমে এড়ানো যায়।
ফলাফল ক্যাশ করার জন্য আমরা একটি ইনস্ট্যান্স ভেরিয়েবল মেমোইজ সেট ব্যবহার করব। এটি প্রথমে চেক করা হয় যে মেমোইজ সেটে n ইতিমধ্যে উপস্থিত আছে কিনা, যদি হ্যাঁ মানটি ফেরত দেওয়া হয়, এবং যদি না হয় মান গণনা করা হয় এবং সেটে যোগ করা হয়।
উদাহরণ
import java.util.HashMap;
import java.util.Map;
public class TutorialPoint {
private Map<Integer, Integer> memoizeSet = new HashMap<>(); // O(1)
public int fibMemoize(int input) {
if (input == 0)
return 0;
if (input == 1)
return 1;
if (this.memoizeSet.containsKey(input)) {
System.out.println("Getting value from computed result for " + input);
return this.memoizeSet.get(input);
}
int result = fibMemoize(input - 1) + fibMemoize(input - 2);
System.out.println("Putting result in cache for " + input);
this.memoizeSet.put(input, result);
return result;
}
public int fibonacci(int n) {
if (n == 0)
return 0;
if (n == 1)
return 1;
System.out.println("Calculating fibonacci number for: " + n);
return (fibonacci(n - 1) + fibonacci(n - 2));
}
public static void main(String[] args) {
TutorialPoint tutorialPoint = new TutorialPoint();
System.out.println("Fibonacci value for n=5: " + tutorialPoint.fibMemoize(5));
}
} আউটপুট
যদি আমরা উপরের কোডটি চালাই তবে এটি নিম্নলিখিত আউটপুট তৈরি করবে
Adding result in memoizeSet for 2 Adding result in memoizeSet for 3 Getting value from computed result for 2 Adding result in memoizeSet for 4 Getting value from computed result for 3 Adding result in memoizeSet for 5
n=5:5
এর জন্য ফিবোনাচি মানদেখা যায় 2 এবং 3 এর জন্য ফিবোনাচি সংখ্যা আবার গণনা করা হয় না। এখানে আমরা মানগুলি সংরক্ষণ করার জন্য একটি হ্যাশম্যাপ মুখস্থের সাথে পরিচয় করিয়ে দিচ্ছি যা ইতিমধ্যেই প্রতিটি ফিবোনাচি গণনা সেটে চেক করার আগে গণনা করা হয়েছে যদি ইনপুটের জন্য মান গণনা করা হয় এবং যদি না থাকে তবে নির্দিষ্ট ইনপুটের মান সেটে যোগ করা হয়।
2-D স্মৃতিচারণ
উপরের প্রোগ্রামে আমাদের শুধুমাত্র একটি অ ধ্রুবক পরামিতি ছিল। নীচের প্রোগ্রামে আমরা একটি রিকার্সিভ প্রোগ্রামের উদাহরণ নেব যার দুটি প্যারামিটার রয়েছে যা প্রতিটি রিকার্সিভ কলের পরে এর মান পরিবর্তন করে এবং আমরা এটিকে অপ্টিমাইজ করার জন্য দুটি নন-কনস্ট্যান্ট প্যারামিটারে মেমোরাইজেশন প্রয়োগ করব। একে 2-ডি মেমোরাইজেশন বলে।
উদাহরণ স্বরূপ:-আমরা স্ট্যান্ডার্ড লংগেস্ট কমন সিক্যুয়েন্স(এলসিএস) বাস্তবায়ন করতে যাচ্ছি .যদি ক্রমগুলির একটি সেট দেওয়া হয়, তবে দীর্ঘতম সাধারণ পরবর্তী সমস্যাটি হল সর্বাধিক দৈর্ঘ্যের সমস্ত ক্রমগুলির একটি সাধারণ অনুবর্তন খুঁজে পাওয়া। সম্ভাব্য সমন্বয় 2n হবে।
উদাহরণ
class TP {
static int computeMax(int a, int b) {
return (a > b) ? a : b;
}
static int longestComSs(String X, String Y, int m, int n) {
if (m == 0 || n == 0)
return 0;
if (X.charAt(m - 1) == Y.charAt(n - 1))
return 1 + longestComSs(X, Y, m - 1, n - 1);
else
return computeMax(longestComSs(X, Y, m, n - 1), longestComSs(X, Y, m - 1, n));
}
public static void main(String[] args) {
String word_1 = "AGGTAB";
String word_2 = "GXTXAYB";
System.out.print("Length of LCS is " + longestComSs(word_1, word_2, word_1.length(),word_2.length()));
}
} আউটপুট
যদি আমরা উপরের কোডটি চালাই তবে এটি নিম্নলিখিত আউটপুট তৈরি করবে
Length of LCS is 4
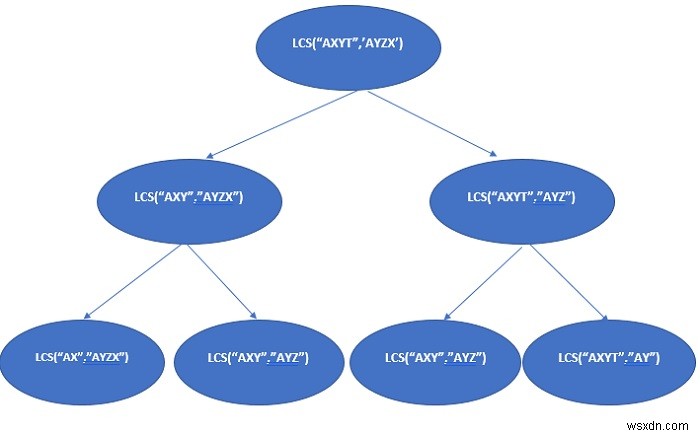
উপরের হাফওয়ে রিকারশন ট্রিতে, lcs("AXY", "AYZ") একাধিকবার সমাধান করা হয়েছে৷
এই সমস্যার ওভারল্যাপিং সাবস্ট্রাকচার বৈশিষ্ট্যের ফলে, একই সাব-সমস্যাগুলির প্রাক গণনা মেমোরাইজেশন বা ট্যাবুলেশন ব্যবহার করে এড়ানো যেতে পারে।
রিকার্সিভ কোডের মেমোরাইজেশন পদ্ধতি নিম্নরূপ প্রয়োগ করা হয়।
উদাহরণ
import java.io.*;
import java.lang.*;
class testClass {
final static int maxSize = 1000;
public static int arr[][] = new int[maxSize][maxSize];
public static int calculatelcs(String str_1, String str_2, int m, int n) {
if (m == 0 || n == 0)
return 0;
if (arr[m - 1][n - 1] != -1)
return arr[m - 1][n - 1];
if (str_1.charAt(m - 1) == str_2.charAt(n - 1)) {
arr[m - 1][n - 1] = 1 + calculatelcs(str_1, str_2, m - 1, n - 1);
return arr[m - 1][n - 1];
}
else {
int a = calculatelcs(str_1, str_2, m, n - 1);
int b = calculatelcs(str_1, str_2, m - 1, n);
int max = (a > b) ? a : b;
arr[m - 1][n - 1] = max;
return arr[m - 1][n - 1];
}
}
public static void main(String[] args) {
for (int i = 0; i < 1000; i++) {
for (int j = 0; j < 1000; j++) {
arr[i][j] = -1;
}
}
String str_1 = "AGGTAB";
String str_2 = "GXTXAYB";
System.out.println("Length of LCS is " + calculatelcs(str_1, str_2, str_1.length(),str_2.length()));
}
} আউটপুট
যদি আমরা উপরের কোডটি চালাই তবে এটি নিম্নলিখিত আউটপুট তৈরি করবে
Length of LCS is 4
পন্থা
এটি দেখা গেছে যে পদ্ধতিতে (calculatelcs) 2টি ধ্রুবক (যা মুখস্থকে প্রভাবিত করে না) এবং 2টি অ ধ্রুবক যুক্তি সহ 4টি যুক্তি রয়েছে (m এবং n) যা প্রতিটি পুনরাবৃত্ত পদ্ধতি কলিং এর মান পরিবর্তন করে। তাই মেমোরাইজেশন অর্জনের জন্য আমরা lcs(m,n) এর গণিত মান arr[m-1][n-1] এ সংরক্ষণ করার জন্য একটি 2-D অ্যারে প্রবর্তন করি। যখনই একই আর্গুমেন্ট m এবং n যুক্ত ফাংশনটি আবার কল করা হয় তখন আমরা আর কোনো রিকার্সিভ কল করি না এবং arr[m-1][n-1] ফেরত দিই, কারণ lcs(m, n) এর পূর্ববর্তী গণনা ইতিমধ্যেই হয়ে গেছে। arr[m-1][n-1]-এ সংরক্ষিত, এইভাবে পুনরাবৃত্ত কলের সংখ্যা কমিয়ে দেয়।
3-D স্মৃতিচারণ
এটি 3টি অ-স্থির আর্গুমেন্ট সহ একটি পুনরাবৃত্ত প্রোগ্রামের জন্য স্মরণীয়করণ অর্জনের একটি পদ্ধতি। এখানে আমরা তিনটি স্ট্রিংয়ের জন্য LCS-এর দৈর্ঘ্য গণনার উদাহরণ নিচ্ছি।
এখানে পন্থা হল প্রদত্ত স্ট্রিংগুলির জন্য সমস্ত সম্ভাব্য অনুক্রম (মোট সম্ভাব্য পরবর্তী 3ⁿ) তৈরি করা এবং তাদের মধ্যে সবচেয়ে দীর্ঘতম সাধারণ অনুগামীর সাথে মিল করা।
আমরা গণনা করা মান সংরক্ষণ করার জন্য একটি 3-ডি টেবিল প্রবর্তন করব। পরবর্তী বিষয়গুলো বিবেচনা করে।
-
A1[1...i] i
-
A2[1...j] j
-
A3[1...k] k
যদি আমরা একটি সাধারণ অক্ষর (X[i]==Y[j]==Z[k]) খুঁজে পাই তবে আমাদের অবশিষ্টগুলি পুনরাবৃত্তি করতে হবে৷ অন্যথায় আমরা নিম্নলিখিত ক্ষেত্রে সর্বাধিক গণনা করব
-
অন্যদের জন্য X[i] পুনরাবৃত্তি করুন
-
অন্যদের জন্য Y[j] পুনরাবৃত্তি করুন
-
অন্যদের জন্য Z[k] পুনরাবৃত্তি করুন
সুতরাং, যদি আমরা উপরের ধারণাটি আমাদের পুনরাবৃত্ত ফাংশনে তৈরি করি তাহলে
f(N,M,K)={1+f(N-1,M-1,K-1) if (X[N]==Y[M]==Z[K]সর্বোচ্চ(f(N-) 1,M,K),f(N,M-1,K),f(N,M,K-1))}
-
f(N-1,M,K) =অন্যদের জন্য X[i] পুনরাবৃত্তি করুন
-
f(N,M-1,K) =Y[j]কে অন্যদের জন্য পুনরাবৃত্তি করুন
-
f(N,M,K-1) =অন্যদের জন্য Z[k] পুনরাবৃত্তি করুন
উদাহরণ
import java.io.IOException;
import java.io.InputStream;
import java.util.*;
class testClass {
public static int[][][] arr = new int[100][100][100];
static int calculatelcs(String str_1, String str_2, String str_3, int m, int n, int o) {
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
arr[i][j][0] = 0;
}
}
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= o; j++) {
arr[0][i][j] = 0;
}
}
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= o; j++) {
arr[i][0][j] = 0;
}
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= o; k++) {
if (str_1.charAt(i - 1) == str_2.charAt(j-1) && str_2.charAt(j1) == str_3.charAt(k-1)) {
arr[i][j][k] = 1 + arr[i - 1][j - 1][k - 1];
}
else {
arr[i][j][k] = calculateMax(arr[i - 1][j][k], arr[i][j - 1][k], arr[i][j][k - 1]);
}
}
}
}
return arr[m][n][o];
}
static int calculateMax(int a, int b, int c) {
if (a > b && a > c)
return a;
if (b > c)
return b;
return c;
}
public static void main(String[] args) {
String str_1 = "clued";
String str_2 = "clueless";
String str_3 = "xcxclueing";
int m = str_1.length();
int n = str_2.length();
int o = str_3.length();
System.out.print("Length of LCS is " + calculatelcs(str_1, str_2, str_3, m, n, o));
}
} আউটপুট
যদি আমরা উপরের কোডটি চালাই তবে এটি নিম্নলিখিত আউটপুট তৈরি করবে
Length of LCS is 4


