ধরুন আমাদের একটি সম্পূর্ণ গ্রাফ আছে; আমাদের এজ ডিসজয়েন্ট স্প্যানিং গাছের সংখ্যা গণনা করতে হবে। এজ ডিসজয়েন্ট স্প্যানিং ট্রি হল স্প্যানিং ট্রি, যেখানে সেটের কোন দুটি গাছের প্রান্তে মিল নেই। ধরুন N (উল্লম্বের সংখ্যা) 4, তাহলে আউটপুট হবে 2। 4টি শীর্ষবিন্দু ব্যবহার করে সম্পূর্ণ গ্রাফটি নিচের মত -
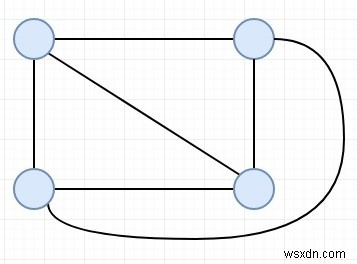
−
এর মত দুই প্রান্ত বিচ্ছিন্ন বিস্তৃত গাছ
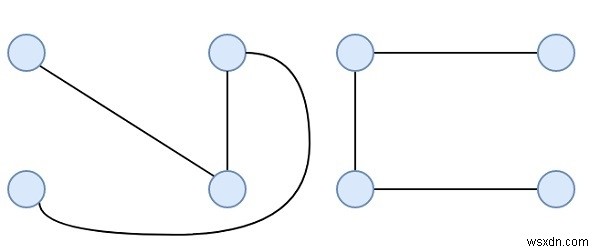
N শীর্ষবিন্দু সহ একটি সম্পূর্ণ গ্রাফ থেকে প্রান্ত বিচ্ছিন্ন বৃক্ষের সর্বাধিক সংখ্যা হবে $[\frac{n}{2}]$
উদাহরণ
#include <iostream>
#include <cmath>
using namespace std;
int maxEdgeDisjointSpanningTree(int n){
return floor(n/2);
}
int main() {
int n = 4;
cout << "Maximum Edge Disjoint Spanning Tree: " <<
maxEdgeDisjointSpanningTree(n);
} আউটপুট
Maximum Edge Disjoint Spanning Tree: 2


