ধরুন আমাদের একটি গ্রাফ আছে। কোসারাজু অ্যালগরিদম ব্যবহার করে গ্রাফটি দৃঢ়ভাবে সংযুক্ত কিনা তা আমাদের পরীক্ষা করতে হবে। একটি গ্রাফকে শক্তিশালীভাবে সংযুক্ত বলা হয়, যদি কোন দুটি শীর্ষবিন্দুর মধ্যে পথ থাকে, তাহলে গ্রাফটি সংযুক্ত। একটি অনির্দেশিত গ্রাফ হল দৃঢ়ভাবে সংযুক্ত গ্রাফ।
কিছু অনির্দেশিত গ্রাফ সংযুক্ত হতে পারে কিন্তু দৃঢ়ভাবে সংযুক্ত নয়। এটি দৃঢ়ভাবে সংযুক্ত গ্রাফের একটি উদাহরণ৷
৷
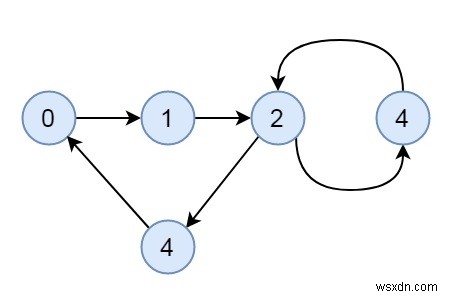
এটি সংযুক্ত, কিন্তু দৃঢ়ভাবে সংযুক্ত গ্রাফের একটি উদাহরণ।
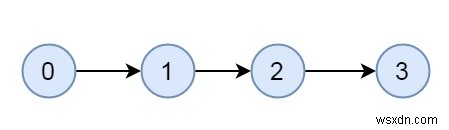
এখানে আমরা দেখব, কোসারাজু অ্যালগরিদমের নিম্নলিখিত ধাপগুলি ব্যবহার করে কীভাবে একটি গ্রাফ দৃঢ়ভাবে সংযুক্ত বা না তা পরীক্ষা করা যায়।
পদক্ষেপ −
-
সমস্ত নোডকে পরিদর্শন করা হয়নি হিসাবে চিহ্নিত করুন
-
যে কোন নির্বিচারে শীর্ষবিন্দু থেকে DFS ট্রাভার্সাল শুরু করুন। যদি DFS সমস্ত নোড পরিদর্শন করতে ব্যর্থ হয়, তাহলে মিথ্যা ফেরত দিন।
-
গ্রাফের সমস্ত প্রান্ত বিপরীত করুন
-
সমস্ত শিরোনাম আবার পরিদর্শন করা নোড হিসাবে সেট করুন
-
যে শীর্ষবিন্দু থেকে DFS ট্রাভার্সাল শুরু করুন u. যদি DFS সমস্ত নোড পরিদর্শন করতে ব্যর্থ হয়, তাহলে মিথ্যা ফেরত দিন। অন্যথায় সত্য।
উদাহরণ
#include <iostream>
#include <list>
#include <stack>
using namespace std;
class Graph {
int V;
list<int> *adj;
void dfs(int v, bool visited[]);
public:
Graph(int V) {
this->V = V;
adj = new list<int>[V];
}
~Graph() {
delete [] adj;
}
void addEdge(int v, int w);
bool isStronglyConnected();
Graph reverseArc();
};
void Graph::dfs(int v, bool visited[]) {
visited[v] = true;
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
if (!visited[*i])
dfs(*i, visited);
}
Graph Graph::reverseArc() {
Graph graph(V);
for (int v = 0; v < V; v++) {
list<int>::iterator i;
for(i = adj[v].begin(); i != adj[v].end(); ++i)
graph.adj[*i].push_back(v);
}
return graph;
}
void Graph::addEdge(int u, int v) {
adj[u].push_back(v);
}
bool Graph::isStronglyConnected() {
bool visited[V];
for (int i = 0; i < V; i++)
visited[i] = false;
dfs(0, visited);
for (int i = 0; i < V; i++)
if (visited[i] == false)
return false;
Graph graph = reverseArc();
for(int i = 0; i < V; i++)
visited[i] = false;
graph.dfs(0, visited);
for (int i = 0; i < V; i++)
if (visited[i] == false)
return false;
return true;
}
int main() {
Graph graph(5);
graph.addEdge(0, 1);
graph.addEdge(1, 2);
graph.addEdge(2, 3);
graph.addEdge(3, 0);
graph.addEdge(2, 4);
graph.addEdge(4, 2);
graph.isStronglyConnected()? cout << "This is strongly connected" : cout << "This is not strongly connected";
} আউটপুট
This is strongly connected


