বাইনারি অনুসন্ধান, অর্ধ-ব্যবধান অনুসন্ধান, লগারিদমিক অনুসন্ধান বা বাইনারি চপ নামেও পরিচিত, একটি অনুসন্ধান অ্যালগরিদম যা একটি সাজানো অ্যারের মধ্যে একটি লক্ষ্য মানের অবস্থান খুঁজে পায়। বাইনারি অনুসন্ধান লক্ষ্য মানকে অ্যারের মধ্যম উপাদানের সাথে তুলনা করে। যদি তারা সমান না হয়, যে অর্ধেকটি লক্ষ্য মিথ্যা হতে পারে না তা বাদ দেওয়া হয় এবং বাকি অর্ধেক অনুসন্ধান চালিয়ে যায়, আবার লক্ষ্য মানের সাথে তুলনা করার জন্য মাঝের উপাদানটি গ্রহণ করে এবং লক্ষ্য মান পাওয়া না যাওয়া পর্যন্ত এটি পুনরাবৃত্তি করে। বাকি অর্ধেক খালি রেখে সার্চ শেষ হলে, টার্গেট অ্যারেতে নেই। যদিও ধারণাটি সহজ, বাইনারি অনুসন্ধান সঠিকভাবে বাস্তবায়নের জন্য এর প্রস্থান অবস্থা এবং মধ্যবিন্দু গণনা সম্পর্কে কিছু সূক্ষ্মতার দিকে মনোযোগ দেওয়া প্রয়োজন, বিশেষ করে যদি অ্যারের মানগুলি পরিসরের সম্পূর্ণ সংখ্যার সমস্ত না হয়৷
বাইনারি সার্চ হল সবচেয়ে জনপ্রিয় সার্চ অ্যালগরিদম। এটি কার্যকরী এবং সবচেয়ে বেশি ব্যবহৃত কৌশলগুলির মধ্যে একটি যা সমস্যা সমাধানের জন্য ব্যবহৃত হয়।
যদি বিশ্বের সমস্ত নাম একসাথে লেখা হয় এবং আপনি একটি নির্দিষ্ট নামের অবস্থান অনুসন্ধান করতে চান, বাইনারি অনুসন্ধান সর্বাধিক 35টি পুনরাবৃত্তিতে এটি সম্পন্ন করবে৷
বাইনারি অনুসন্ধান শুধুমাত্র উপাদানগুলির একটি সাজানো সেটে কাজ করে। একটি সংগ্রহে বাইনারি অনুসন্ধান ব্যবহার করতে, সংগ্রহটি প্রথমে সাজাতে হবে৷
যখন একটি বাইনারি অনুসন্ধান একটি সাজানো সেটে ক্রিয়াকলাপ সম্পাদন করতে ব্যবহৃত হয়, তখন যে মানের অনুসন্ধান করা হচ্ছে তার ভিত্তিতে পুনরাবৃত্তির সংখ্যা সর্বদা হ্রাস করা যেতে পারে।
আসুন আমরা নিম্নলিখিত অ্যারেটি বিবেচনা করি -

একটি রৈখিক অনুসন্ধান ব্যবহার করে, উপাদান 8 এর অবস্থান 9ম পুনরাবৃত্তিতে নির্ধারিত হবে৷
আসুন দেখি কিভাবে বাইনারি অনুসন্ধান ব্যবহার করে পুনরাবৃত্তির সংখ্যা কমানো যায়। আমরা অনুসন্ধান শুরু করার আগে, আমাদের পরিসরের শুরু এবং শেষ জানতে হবে। আসুন তাদের নিম্ন এবং উচ্চ বলি।
Low = 0 High = n-1
এখন, নিম্ন এবং উপরের সীমানার মধ্যবর্তী স্থানে অবস্থিত উপাদানটির সাথে অনুসন্ধান মান K তুলনা করুন। মান K বেশি হলে, নিম্ন সীমানা বাড়ান, অন্যথায় উপরের সীমানা কমিয়ে দিন।
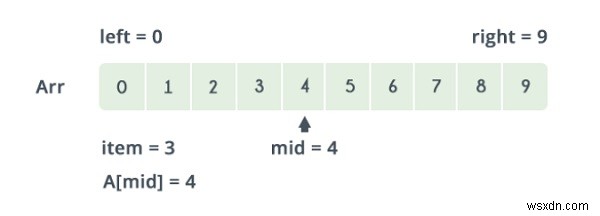
উপরের চিত্রটি উল্লেখ করে, নীচের সীমাটি 0 এবং উপরের সীমাটি 9
নিম্ন এবং উপরের সীমার মধ্যক হল (lower_bound + upper_bound) / 2 =4. এখানে a[4] =4. মান 4>2, যা আপনি যে মানটি খুঁজছেন। অতএব, আমাদের 4 এর বাইরে কোনো উপাদানের উপর অনুসন্ধান চালানোর প্রয়োজন নেই কারণ এর বাইরের উপাদানগুলি অবশ্যই 2 এর থেকে বেশি হবে৷
অতএব, আমরা সর্বদা অ্যারের উপরের বাউন্ডটিকে 4 এলিমেন্টের অবস্থানে নামাতে পারি। এখন, আমরা নিম্নলিখিত মানগুলির সাথে একই অ্যারেতে একই পদ্ধতি অনুসরণ করি -
Low: 0 High: 3
নিম্ন> উচ্চ পর্যন্ত এই পদ্ধতিটি পুনরাবৃত্তি করুন। যদি কোনো পুনরাবৃত্তিতে, আমরা একটি [mid]=কী পাই, আমরা মধ্য-এর মান ফেরত দিই। এটি অ্যারেতে কী এর অবস্থান। যদি অ্যারেতে কী উপস্থিত না থাকে, আমরা −1 ফেরত দিই।
উদাহরণ
int binarySearch(int low,int high,int key){
while(low<=high){
int mid=(low+high)/2;
if(a[mid]<key){
low=mid+1;
}
else if(a[mid]>key){
high=mid-1;
}
else{
return mid;
}
}
return -1; //key not found
} 

