একটি BST বা বাইনারি সার্চ ট্রি হল বাইনারি ট্রির একটি ফর্ম যার সমস্ত বাম নোড ছোট এবং সমস্ত ডান নোড রুট মানের থেকে বড়। এই সমস্যার জন্য, আমরা একটি বাইনারি ট্রি নেব এবং এতে বর্তমান নোডের চেয়ে বড় সমস্ত মান যুক্ত করব। "BST-এর প্রতিটি নোডে সব বৃহত্তর মান যোগ করুন" সমস্যাটিকে সরলীকৃত করা হয়েছে কারণ একটি BST-এর জন্য সেই নোডের মানটিতে বর্তমান নোডের মানের থেকে বড় সমস্ত নোডের মান যোগ করুন৷
BST প্রবলেম স্টেটমেন্ট -
-এ প্রতিটি নোডে সব বড় মান যোগ করুনএকটি বাইনারি সার্চ ট্রি (BST) দেওয়া হয়েছে, আমাদের প্রতিটি নোডে যোগ করতে হবে, সমস্ত বড় মানের নোডের সমষ্টি৷
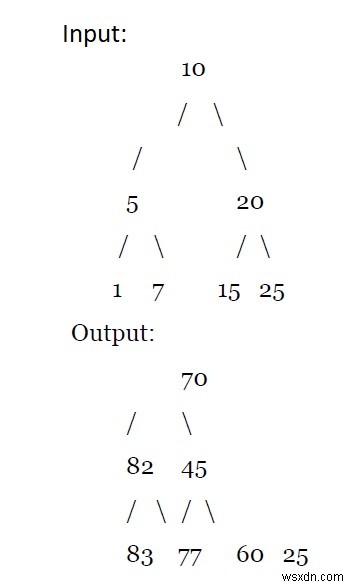
ব্যাখ্যা
এই প্রোগ্রামটি একটি BST-কে একটি বাইনারি ট্রিতে রূপান্তরিত করবে যার একটি নোডের মান সহ সমস্ত বৃহত্তর উপাদানের যোগফল এবং নোডের আসল মান।
বাইনারি সার্চ ট্রি সলিউশন −
-এ প্রতিটি নোডে সব বৃহত্তর মান যোগ করুনআমরা রিভার্স ইনঅর্ডার ট্র্যাভার্সাল ব্যবহার করি (বাম সাবট্রির পরিবর্তে ডান সাবট্রিতে রিকারশনকে প্রথমে বলা হয়) এবং এ পর্যন্ত যে নোডগুলি অতিক্রম করা হয়েছে তার সমষ্টি সংরক্ষণ করার জন্য একটি পরিবর্তনশীল বজায় রাখি।
তারপর আমরা আমাদের বর্তমান নোডের মান পরিবর্তন করতে এই যোগফল ব্যবহার করি, প্রথমে যোগফলের সাথে এর মান যোগ করে, এবং তারপর এই যোগফলের সাথে নোডের মান প্রতিস্থাপন করে।
উদাহরণ
#include <iostream >
using namespace std;
struct node{
int data;
node *left;
node *right;
};
node *newNode(int key){
node *temp=new node;
temp->left=NULL;
temp->right=NULL;
temp->data=key;
return temp;
}
void Inorder(node *root){
if(!root)
return;
Inorder(root->left);
cout<<root->data<<" ";
Inorder(root->right);
}
node *Insert(node *root,int key){
if(!root)
return newNode(key);
if(key<root->data)
root->left=Insert(root->left,key);
else
root->right=Insert(root->right,key);
return root;
}
void RevInorderAdd(node *root,int &sum){
if(!root)
return;
RevInorderAdd(root->right,sum);
sum+=root->data;
root->data=sum;
RevInorderAdd(root->left,sum);
}
void AddGreater(node *root){
int sum=0;
RevInorderAdd(root,sum);
}
int main() {
/* Let us create following BST
10
/ \
5 20
/ \ / \
1 7 15 25 */
node *root = NULL;
root = Insert(root, 10);
Insert(root, 20);
Insert(root, 25);
Insert(root, 15);
Insert(root, 5);
Insert(root, 7);
Insert(root, 1);
Inorder(root);
cout<<endl;
AddGreater(root);
Inorder(root);
cout<<endl;
return 0;
} 

