দ্বিখণ্ডন পদ্ধতির জন্য C++ প্রোগ্রাম

a এবং b সংখ্যার সাথে f(x) ফাংশন দেওয়া হয়েছে যেখানে, f(a) * f(b)> 0 এবং ফাংশন f(x) a এবং b এর মধ্যে থাকা উচিত অর্থাৎ f(x) =[a, b ]। কাজটি হল দ্বিখণ্ডন পদ্ধতি ব্যবহার করে f(x) ফাংশনে ব্যবধান a এবং b এর মধ্যে থাকা রুটের মান খুঁজে বের করা।

দ্বিখণ্ডন পদ্ধতি কি?

দ্বিখণ্ডিত পদ্ধতিটি 'a' এবং 'b' দ্বারা সংজ্ঞায়িত প্রদত্ত সীমার মধ্যে f(x) ফাংশনে একটি মূলের মান খুঁজে পেতে ব্যবহৃত হয়। ফাংশনের মূলটিকে একটি মান হিসাবে সংজ্ঞায়িত করা যেতে পারে যেমন f(a) =0.

উদাহরণ

Quadratic equation F(x) =  - 8
This equation is equals to 0 when the value of x will be 2 i.e.  - 8 = 0
So, root of this quadratic function F(x) will be 2.

এখন, যদি একটি ফাংশন f(x) প্রদত্ত ব্যবধানে অবিচ্ছিন্ন থাকে [a..b] এবং এছাড়াও, f(a) এর চিহ্ন ≠ f(b) এর চিহ্ন, তাহলে একটি মান m হবে যা ব্যবধান a এর অন্তর্গত। এবং b যেমন f(m) =0

মান m [a..b] যেমন f(m) =0

অর্থাৎ m হল রুটের মান যা একাধিক হতে পারে

নিচের চিত্রটি দেওয়া হল যা f(a) এবং f(b) ব্যবধান দেখায়। এই ব্যবধানগুলির মধ্যে মূল খুঁজে বের করার জন্য সীমাটি অংশে বিভক্ত এবং ভেরিয়েবল m অর্থাৎ

m =(a + b) / 2

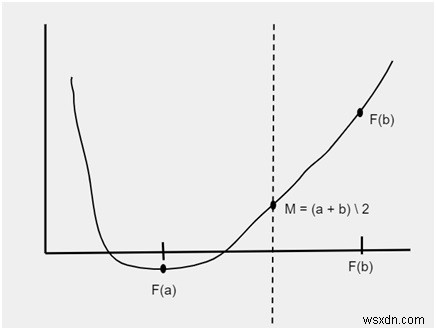
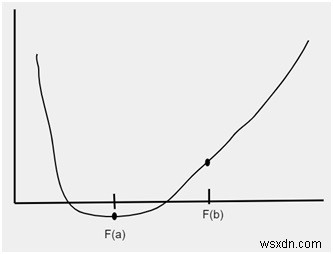
সীমা বিভাজনের পরে নিচের চিত্রে দেখানো হিসাবে নতুন ব্যবধান তৈরি হবে

উদাহরণ

Input-: x^3 - x^2 + 2 ; a =-500 and b = 100
Output-: The value of root is : -0.991821
Input-: x^3 - x^2 + 2 ; a =-200 and b = 300
Output-: The value of root is : -1.0025

আমরা নীচের প্রোগ্রামে যে পদ্ধতি ব্যবহার করছি তা হল অনুসরণ −

• সমীকরণটি ইনপুট করুন এবং a এবং b ব্যবধানের মান
• ব্যবধানগুলিকে এভাবে ভাগ করুন :m =(a + b) / 2
  • প্রিন্ট m হল রুট
• যদি f(m) ≠ 0
  • f(a) * f(m) <0
  কিনা পরীক্ষা করুন
  • তাহলে রুটটি a এবং m এর মধ্যে থাকবে
  • চেক করুন যদি f(b) * f(m) <0
  • তখন রুটটি b এবং m এর মধ্যে থাকবে

অ্যালগরিদম

Start
Step 1-> In function double solution(double x)
   Return x*x*x - x*x + 2
Step 2-> In function bisection(double a, double b)
   If solution(a) * solution(b) >= 0 then,
      Print "You have not assumed right a and b "
      Return
   End If
   Set c = a
   Loop While (b-a) >= EP
      Set c = (a+b)/2
      If solution(c) == 0.0
         Break
      End If
      Else if solution(c)*solution(a) < 0
         Set b = c
      End Else If
      Else
         Set a = c
      End Else
   End
   Print "The value of root”
Step 3-> In function int main()
   Declare and Initialize inputs  a =-500, b = 100
   Call function bisection(a, b)
Stop

উদাহরণ

#include <iostream>
using namespace std;
#define EP 0.01
// An example function whose solution is determined using
// Bisection Method. The function is x^3 - x^2 + 2
double solution(double x) {
   return x*x*x - x*x + 2;
}
// Prints root of solution(x) with error in EPSILON
void bisection(double a, double b) {
   if (solution(a) * solution(b) >= 0) {
      cout << "You have not assumed right a and b\n";
      return;
   }
   double c = a;
   while ((b-a) >= EP) {
      // Find middle point
      c = (a+b)/2;
      // Check if middle point is root
      if (solution(c) == 0.0)
         break;
       // Decide the side to repeat the steps
      else if (solution(c)*solution(a) < 0)
         b = c;
      else
         a = c;
   }
   cout << "The value of root is : " << c;
}
 // main function
int main() {
   double a =-500, b = 100;
   bisection(a, b);
   return 0;
}

আউটপুট

The value of root is : -0.991821