Quicksort হল একটি সাজানোর কৌশল যা একটি সাজানো তালিকা (অ্যারে) সাজানোর জন্য তুলনা ব্যবহার করে। Quicksort পার্টিশন এক্সচেঞ্জ সর্ট নামেও পরিচিত।
এটি একটি স্থিতিশীল বাছাই নয়, কারণ সমান সাজানোর আইটেমের আপেক্ষিক ক্রম সংরক্ষিত হয় না। Quicksort একটি অ্যারেতে কাজ করতে পারে, বাছাই করার জন্য অল্প পরিমাণে মেমরির প্রয়োজন হয়। এটি নির্বাচন সাজানোর অনুরূপ, এটি সর্বদা সবচেয়ে খারাপ-কেস পার্টিশন বেছে নেয় না। সুতরাং, তাই আমরা এটিকে বেছে নেওয়ার সাজানোর একটি ভাল গঠন হিসাবে নিতে পারি।
QuickSort হল সবচেয়ে দক্ষ বাছাই করার অ্যালগরিদমগুলির মধ্যে একটি এবং এটি একটি অ্যারেকে ছোট আকারে বিভক্ত করার উপর ভিত্তি করে। নামটি এই সত্য থেকে এসেছে যে Quicksort সাধারণ বাছাই অ্যালগরিদমগুলির তুলনায় উল্লেখযোগ্যভাবে দ্রুত ডেটা উপাদানগুলির একটি তালিকা বাছাই করতে সক্ষম। এবং মার্জ সর্টের মতো, কুইক সর্টও সমস্যা-সমাধান পদ্ধতির ডিভাইড অ্যান্ড কনক্যুয়ার অ্যাপ্রোচের বিভাগে পড়ে।
Quicksort অ্যালগরিদম নিম্নলিখিত উপায়ে কাজ করে
-
পরিপ্রেক্ষিতে সাদৃশ্যমূলক দৃষ্টিভঙ্গি গ্রহণ করে, এমন একটি পরিস্থিতি বিবেচনা করুন যেখানে একজনকে নাম অনুসারে শিক্ষার্থীদের নাম সহ কাগজপত্র বাছাই করতে হয়েছিল। কেউ নিম্নরূপ পদ্ধতি ব্যবহার করতে পারে -
-
একটি বিভাজন মান নির্বাচন করুন, L বলুন। বিভাজন মানটি পিভট নামেও পরিচিত।
-
কাগজপত্রের স্তুপকে দুই ভাগে ভাগ করুন। A-L এবং M-Z. পাইলস সমান হওয়া জরুরী নয়।
-
A-L পাইলের সাথে উপরের দুটি ধাপের পুনরাবৃত্তি করুন, এটিকে এর উল্লেখযোগ্য দুটি অংশে বিভক্ত করুন। এবং M-Z গাদা, তার অর্ধেক বিভক্ত. প্রক্রিয়াটি পুনরাবৃত্তি করা হয় যতক্ষণ না গাদাগুলি সহজে সাজানোর জন্য যথেষ্ট ছোট হয়।
-
শেষ পর্যন্ত, ছোট স্তূপগুলিকে একটির উপরে অন্যটির উপরে স্থাপন করা যেতে পারে যাতে একটি সম্পূর্ণ সাজানো এবং অর্ডারকৃত কাগজপত্র তৈরি করা যায়।
-
-
এখানে ব্যবহৃত পদ্ধতি হল পুনরাবৃত্তি একক-উপাদান অ্যারে পেতে প্রতিটি বিভাজনে।
-
প্রতিটি বিভাজনে, গাদাটি বিভক্ত করা হয়েছিল এবং তারপরে ছোট পাইলের জন্য একই পদ্ধতি ব্যবহার করা হয়েছিল।
-
এই বৈশিষ্ট্যগুলির কারণে, Quicksort কে পার্টিশন এক্সচেঞ্জ সর্টও বলা হয় .
Input: arr[] = {7,4,2,6,3,1,5}
Output: 1 2 3 4 5 6 7 ব্যাখ্যা
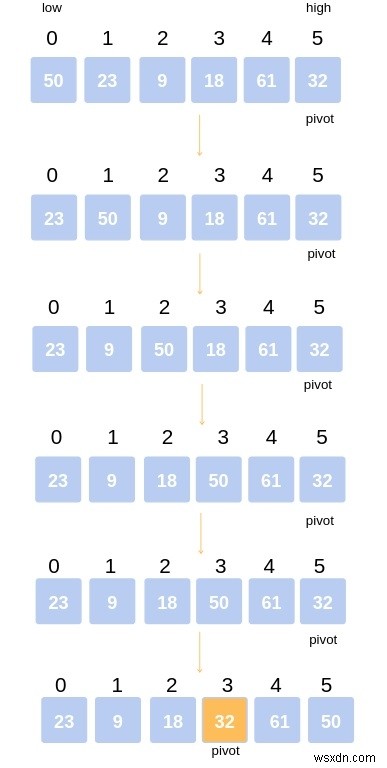
ধারণাটি বোঝার জন্য একটি উদাহরণ কার্যকর হতে পারে। নিম্নলিখিত অ্যারে বিবেচনা করুন:50, 23, 9, 18, 61, 32
ধাপ 1 − তালিকা থেকে পিভট হওয়ার জন্য যেকোনো মান নির্ধারণ করুন (সাধারণত শেষ মান)। ধরুন দুটি মান "নিম্ন" এবং "উচ্চ" প্রথম সূচক এবং শেষ সূচকের সাথে সম্পর্কিত।
আমাদের ক্ষেত্রে কম হল 0 এবং উচ্চ হল 5৷
৷নিম্ন এবং উচ্চ মান হল 50 এবং 32 এবং পিভটের মান হল 32৷
তাই, পার্টিশনের জন্য কল করুন, অ্যারেটিকে এমনভাবে সাজান যাতে পিভট (32) তার আসল অবস্থানে আসে। এবং পিভটের বাম দিকে, অ্যারের সমস্ত উপাদানগুলি এর থেকে কম এবং ডানদিকে এটির চেয়ে বড়৷
পার্টিশন ফাংশনে, আমরা প্রথম উপাদান থেকে শুরু করি এবং পিভটের সাথে তুলনা করি। যেহেতু 50 32-এর থেকে বড়, তাই আমরা কোনও পরিবর্তন করি না এবং পরবর্তী উপাদান 23-এ চলে যাই।
পিভটের সাথে আবার তুলনা করুন। যেহেতু 23 32 এর কম, তাই আমরা 50 এবং 23 অদলবদল করি। অ্যারে 23, 50, 9, 18, 61, 32 হয়ে যায়।
আমরা পরবর্তী এলিমেন্ট 9-এ চলে যাই যা আবার পিভট (32) থেকে কম তাই এটিকে 50 দিয়ে অদলবদল করলে আমাদের অ্যারে হয়ে ওঠে
23, 9, 50, 18, 61, 32।
একইভাবে, পরবর্তী উপাদান 18-এর জন্য যা 32-এর কম, অ্যারে হয়ে যায়
23, 9, 18, 50, 61, 32 এখন 61 পিভট (32) থেকে বড়, তাই কোন পরিবর্তন নেই৷
অবশেষে, আমরা আমাদের পিভটকে 50 দিয়ে অদলবদল করি যাতে এটি সঠিক অবস্থানে আসে।
এইভাবে পিভট (32) তার আসল অবস্থানে আসে এবং এর বাম দিকের সমস্ত উপাদান কম, এবং ডানদিকের সমস্ত উপাদান নিজের থেকে বড়৷
ধাপ 2 − তাই প্রথম ধাপের পরে অ্যারে
হয়ে যায়23, 9, 18, 32, 61, 50, পিভট হিসাবে 32 নিচ্ছে।
ধাপ 3 - এখন তালিকাটি দুটি ভাগে বিভক্ত:
1. পিভটের আগে সাবলিস্ট:23, 9, 18
2. পিভটের পরে সাবলিস্ট:61, 50
পদক্ষেপ 4৷ − এই সাবলিস্টগুলির জন্য আবার পদক্ষেপগুলি পুনরাবৃত্তি করুন৷
৷এইভাবে চূড়ান্ত অ্যারে 9, 18, 23, 32, 50, 61 হয়ে যায়।
উদাহরণ
#include <stdio.h>
void swap(int *a, int *b) {
int temp;
temp = *a;
*a = *b;
*b = temp;
}
int Partition(int a[], int low, int high) {
int pivot, index, i;
index = low;
pivot = high;
for(i=low; i < high; i++) {
if(a[i] < a[pivot]) {
swap(&a[i], &a[index]);
index++;
}
}
swap(&a[pivot], &a[index]);
return index;
}
int RandomPivotPartition(int a[], int low, int high) {
int pvt, n, temp;
n = rand();
pvt = low + n%(high-low+1);
swap(&a[high], &a[pvt]);
return Partition(a, low, high);
}
int QuickSort(int a[], int low, int high) {
return 0;
}
int main() {
int n, i;
n=7;
int arr[]={7,4,2,6,3,1,5};
int high = n-1;
int low = 0 ;
int pindex;
if(low < high) {
pindex = RandomPivotPartition(arr, low, high);
QuickSort(arr, low, pindex-1);
QuickSort(arr, pindex+1, high);
}
for (i = 0; i < n; i++)
printf("%d ", arr[i]);
return 0;
} 

