প্রদত্ত বিন্দু A এবং B লাইন AB এবং পয়েন্ট P এবং Q লাইন PQ এর সাথে সম্পর্কিত; কাজ হল এই দুটি লাইনের মধ্যে ছেদ বিন্দু খুঁজে বের করা।
দ্রষ্টব্য − পয়েন্টগুলি X এবং Y স্থানাঙ্কে 2D সমতলে দেওয়া হয়৷
৷
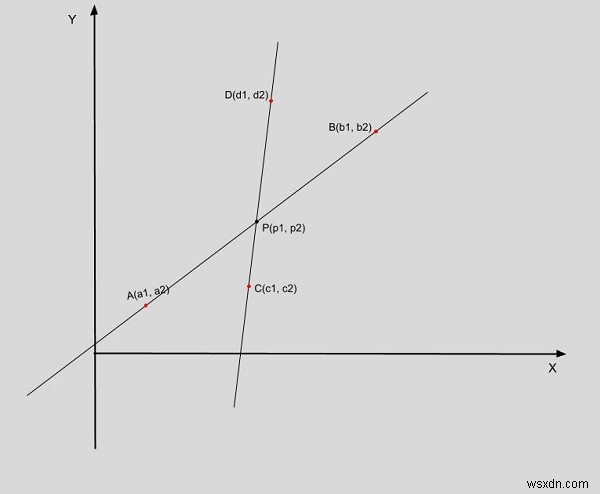
এখানে A(a1, a2), B(b1, b2) এবং C(c1, c2), D(d1, d2) হল স্থানাঙ্ক যা দুটি স্বতন্ত্র রেখা তৈরি করছে এবং P(p1, p2) হল ছেদ বিন্দু। (শুধু ছেদ বিন্দুর চিত্রগত ব্যাখ্যার জন্য)
কিভাবে ছেদ বিন্দু খুঁজে বের করতে হয় −
উপরের চিত্রটিকে −
হিসাবে ধরিউদাহরণ
So using the (a1, a2), (b1, b2), (c1, c2), (d1, d2) We will calculate : A1 = b2 - a2 B1 = a1 - b1 C1 = (A1 * a1) + (B1 * a1) A2 = d2 - c2 B2 = c1 - d1 C2 = (A2 * c1) + (B2 * c2) Let the given lines be: 1. A1x + B1y = C1 2. A2x + B2y = C2 Now, to find the point of intersection, we have to solve these 2 equations. We will multiply 1 by B1 and 2 by B2, so we will get: A1B2x +B1B2y = C1B2 A1B1x +B2B1y = C1B1 Subtracting these we get, (A1B2 - A2B1)x = C1B2-C2B1
এটি আমাদের x এর মান দেয়, এবং একইভাবে আমরা y এর মান পাব যা p1 ছেদ বিন্দু হবে যা x এবং p2 যা y।
দ্রষ্টব্য − উপরের সূত্রটি দুটি লাইনের ছেদ বিন্দু দেবে, কিন্তু যদি রেখার পরিবর্তে রেখাগুলি দেওয়া হয়, তাহলে আমাদের সেই বিন্দুটিকে পুনরায় পরীক্ষা করতে হবে যাতে গণনাকৃত ফলাফলটি লাইনের অংশে থাকা আবশ্যক৷
- মিনিট (x1, x2) <=x <=সর্বোচ্চ (x1, x2)
- মিনিট (y1, y2) <=y <=সর্বোচ্চ (y1, y2)
উপরের সমস্যা সমাধানের জন্য আমরা যে পদ্ধতি ব্যবহার করছি -
- ইনপুট মান নিন।
- নির্ধারকটি খুঁজুন যা a1 * b2 - a2 * b1
- নির্ধারক =0 হলে রেখাগুলি সমান্তরাল কিনা তা পরীক্ষা করুন
- যদি নির্ধারক শূন্য না হয় তাহলে x =(c1 * b2 - c2 * b1) এবং y =(a1 * c2 - a2 * c1)
- ফলাফল প্রিন্ট করুন।
অ্যালগরিদম
Start Step 1-> Declare function to print the x and y coordinates void display(mk_pair par) Print par.first and par.second Step 2-> declare function to calculate the intersection point mk_pair intersection(mk_pair A, mk_pair B, mk_pair C, mk_pair D) Declare double a = B.second - A.second Declare double b = A.first - B.first Declare double c = a*(A.first) + b*(A.second) Declare double a1 = D.second - C.second Declare double b1 = C.first - D.first Declare double c1 = a1*(C.first)+ b1*(C.second) Declare double det = a*b1 - a1*b IF (det = 0) return make_pair(FLT_MAX, FLT_MAX) End Else Declare double x = (b1*c - b*c1)/det Declare double y = (a*c1 - a1*c)/det return make_pair(x, y) End Step 3-> In main() Declare and call function for points as mk_pair q = make_pair(2, 1) IF (inter.first = FLT_MAX AND inter.second = FLT_MAX) Print “given lines are parallel“ End Else Call display(inter) End Stop
উদাহরণ
#include <bits/stdc++.h>
using namespace std;
#define mk_pair pair<double, double>
//display the x and y coordinates
void display(mk_pair par) {
cout << "(" << par.first << ", " << par.second << ")" << endl;
}
mk_pair intersection(mk_pair A, mk_pair B, mk_pair C, mk_pair D) {
// Line AB represented as a1x + b1y = c1
double a = B.second - A.second;
double b = A.first - B.first;
double c = a*(A.first) + b*(A.second);
// Line CD represented as a2x + b2y = c2
double a1 = D.second - C.second;
double b1 = C.first - D.first;
double c1 = a1*(C.first)+ b1*(C.second);
double det = a*b1 - a1*b;
if (det == 0) {
return make_pair(FLT_MAX, FLT_MAX);
} else {
double x = (b1*c - b*c1)/det;
double y = (a*c1 - a1*c)/det;
return make_pair(x, y);
}
}
int main() {
mk_pair q = make_pair(2, 1);
mk_pair r = make_pair(2, 7);
mk_pair s = make_pair(4, 4);
mk_pair t = make_pair(6, 4);
mk_pair inter = intersection(q, r, s, t);
if (inter.first == FLT_MAX && inter.second==FLT_MAX) {
cout << "The given lines AB and CD are parallel.\n";
} else {
cout << "The intersection of the given lines AB and CD is: ";
display(inter);
}
return 0;
} আউটপুট
The intersection of the given lines AB and CD is: (2, 4)


