একটি 2-3 গাছকে একটি ট্রি ডেটা স্ট্রাকচার হিসাবে সংজ্ঞায়িত করা হয়, যেখানে প্রতিটি নোডে বাচ্চাদের (অভ্যন্তরীণ নোড) দুটি শিশু (2-নোড) পাশাপাশি একটি ডেটা উপাদান বা তিনটি শিশু (3-নোড) পাশাপাশি দুটি ডেটা থাকে উপাদান।
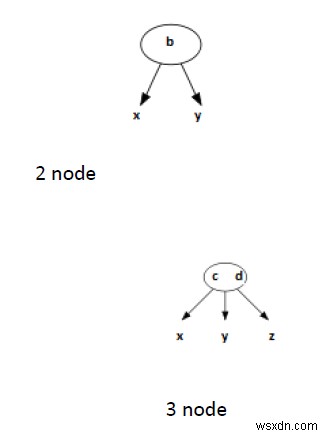
সংজ্ঞা
আমরা বলি যে একটি অভ্যন্তরীণ নোড হল 2-নোড যদি এতে একটি ডেটা উপাদান এবং দুটি শিশু থাকে।
আমরা বলি যে একটি অভ্যন্তরীণ নোড একটি 3-নোড যদি এতে দুটি ডেটা উপাদান এবং তিনটি শিশু থাকে।
আমরা বলি যে T একটি 2-3 গাছ যদি এবং শুধুমাত্র যদি নিম্নলিখিত বিবৃতিগুলির মধ্যে একটি সন্তুষ্ট হয় −
-
T খালি বা খালি। অন্য কথায়, T-এ কোন নোড নেই।
-
T একটি 2-নোড যা ডেটা উপাদান a দিয়ে সজ্জিত। যদি T বাম সন্তান L এবং ডান সন্তান R থাকে, তাহলে আমরা উপসংহারে পৌঁছাই
-
L এবং R একই উচ্চতার 2-3টি বৃক্ষ অ-শূন্য হিসাবে ধরা হয়;
-
একটি এল প্রতিটি উপাদানের চেয়ে বেশি; এবং
-
a R.
-এর প্রতিটি ডেটা উপাদানের চেয়ে ছোট বা সমান -
T হল একটি 3-নোড যার ডেটা উপাদান a এবং b, যেখানে a b এর থেকে কম। যদি T বাম সন্তান L, মধ্যম সন্তান M এবং ডান সন্তান R থাকে, তাহলে আমরা উপসংহারে পৌঁছাই
-
L, M, এবং R সমান উচ্চতার 2-3টি বৃক্ষ খালি নয় বলে ধরা হয়;
-
a L-এর প্রতিটি ডেটা উপাদানের চেয়ে বেশি এবং M-এর প্রতিটি ডেটা উপাদানের চেয়ে ছোট বা সমান; এবং
-
b হল M-এর প্রতিটি ডেটা উপাদানের থেকে বেশি এবং R.
-এর প্রতিটি ডেটা উপাদানের থেকে ছোট বা সমান
সম্পত্তি
-
প্রতিটি অভ্যন্তরীণ নোডকে 2-নোড বা 3-নোড হিসাবে বিবেচনা করা হয়।
-
সমস্ত পাতা একই স্তরে অবস্থিত।
-
সমস্ত ডেটা রক্ষণাবেক্ষণ বা সাজানো ক্রমে রাখা হয়।
অপারেশনগুলি
অনুসন্ধান করা হচ্ছে
একটি 2-3 গাছে একটি আইটেম অনুসন্ধান করা একটি বাইনারি অনুসন্ধান গাছে একটি আইটেম অনুসন্ধান করার মতোই৷ যেহেতু প্রতিটি নোডের ডেটা উপাদানগুলিকে ক্রমানুসারে বিবেচনা করা হয়, তাই একটি অনুসন্ধান ফাংশন সঠিক সাবট্রিতে এবং শেষ পর্যন্ত আইটেমটি নিয়ে গঠিত সঠিক নোডে নির্দেশিত হবে৷
-
T-কে 2-3 ট্রি হিসাবে ধরা যাক এবং d হল সেই ডেটা উপাদান যা আমরা খুঁজে পেতে চাই। যদি T খালি হয়, তাহলে d টি T-এ নেই এবং আমরা সঞ্চালিত হই।
-
r কে T এর মূল হিসাবে ধরা যাক।
-
ধরুন r একটি পাতা। যদি d r তে না থাকে, ফলস্বরূপ d টি T-তে নেই। অন্যথায়, d টি T-তে থাকে। বিশেষ করে, d একটি পাতার নোডে পাওয়া যেতে পারে। আমাদের আর কোন পদক্ষেপের প্রয়োজন নেই এবং আমরা সঞ্চালিত হয়েছি।
-
ধরুন r কে বাম চাইল্ড L এবং ডান চাইল্ড R এর সাথে একটি 2-নোড হিসাবে বিবেচনা করা হয়।
তিনটি ক্ষেত্রে আছে -
-
যদি d এর সমান হয়, তাহলে আমরা T-তে d খুঁজে পেয়েছি এবং আমরা পারফর্ম করেছি।
-
যদি d ই এর থেকে কম হয়, তাহলে T-কে L সেট করুন, যেটি সংজ্ঞা অনুসারে একটি 2-3 গাছ, এবং ধাপ 2 এ ফিরে যান।
-
যদি d বড় হয় e, তাহলে T তে R সেট করুন এবং ধাপ 2 এ ফিরে যান।
-
ধরুন r হল একটি 3-নোড যার বাম সন্তান L, মধ্যম সন্তান M এবং ডান চাইল্ড R। ধরা যাক a এবং b কে r-এর দুটি ডেটা উপাদান হিসাবে ধরা যাক, যেখানে a
-
যদি d a বা b এর সমান হয়, তাহলে d টি T-এ থাকে এবং আমরা পারফর্ম করি।
-
যদি d a এর থেকে কম হয়, তাহলে T-কে L সেট করুন এবং ধাপ 2 এ ফিরে যান।
-
যদি ais d-এর থেকে কম হয় এবং d-এর থেকে কম হয়, তাহলে T-কে M-এ সেট করুন এবং ধাপ 2-এ ফিরে যান।
-
d যদি b-এর থেকে বড় হয়, তাহলে T-কে R-এ সেট করুন এবং ধাপ 2-এ ফিরে যান।
-
সন্নিবেশ
সন্নিবেশ কীটির সঠিক অবস্থান অনুসন্ধান করে এবং সেখানে যোগ বা যোগ করে সঞ্চালিত হয়। যদি নোডটি 4-নোড হয়ে যায় তাহলে নোডটি দুটি 2-নোডে বিভক্ত হয় এবং মাঝের কীটি প্যারেন্ট পর্যন্ত সরানো হয়। অভিভাবক তখন একটি 4-নোড হয়ে উঠতে পারে, এই ক্ষেত্রে এটিও বিভক্ত হয়, তার নিজের অভিভাবকের কাছে একটি কী প্রচার করে। এই প্রক্রিয়াটি পুনরাবৃত্তি হয় যতক্ষণ না আমরা একটি অভিভাবকের কাছে পৌঁছাই যা একটি 2-নোড এবং বিভক্ত করার প্রয়োজন নেই, বা যখন আমরা রুটে পৌঁছাই, এই ক্ষেত্রে আমরা একটি নতুন রুট তৈরি করতে প্রচারিত উপাদানটি প্রয়োগ করি যা একটি 2-নোড। . এই অ্যালগরিদমের সাহায্যে, সঞ্চালনের সংখ্যা গাছের উচ্চতার সমানুপাতিক, তাই লগারিদমিক কারণ গাছটি পুরোপুরি ভারসাম্যপূর্ণ। প্রক্রিয়াটি নিশ্চিত করে যে এর ফলাফলটি 2-3টি গাছ হিসাবে বিবেচিত হয়:বিশেষ করে, সমস্ত পাতা একই গভীরতায় থাকে।
নীচের চিত্রটি এই প্রক্রিয়ার সম্ভাব্য ক্ষেত্রে ব্যাখ্যা করে বা চিত্রিত করে।
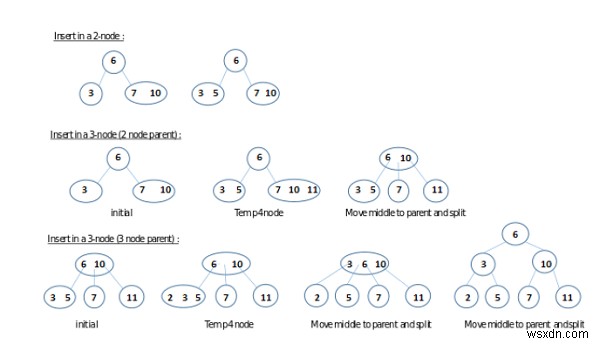
3টি সম্ভাব্য ক্ষেত্রে একটি 2-3 গাছে একটি সংখ্যা সন্নিবেশ করান৷


