ধরুন f =(x1 ∨ y1) ∧ (x2 ∨ y2) ∧ ... ∧ (xn ∨ yn)।
সমস্যা:f কি সন্তোষজনক?
xi ∨ yi এবং  এবং
এবং 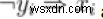
সব সমতুল্য। তাই আমরা প্রতিটি (xi ∨ yi) s কে ঐ দুটি বিবৃতিতে রূপান্তর করছি।
এখন 2n শীর্ষবিন্দু সহ একটি গ্রাফ অনুমান করুন। প্রতিটি (xi∨yi) এর ক্ষেত্রে দুটি নির্দেশিত প্রান্ত যোগ করা হয়
-
¬xi থেকে yi
-
¬yi থেকে xi
¬xi এবং xi উভয়ই একই SCC (স্ট্রংলি কানেক্টেড কম্পোনেন্ট) এ থাকলে f সন্তোষজনক বলে ধরা হয় না
অনুমান করুন যে f কে সন্তোষজনক হিসাবে বিবেচনা করা হয়। এখন আমরা f সন্তুষ্ট করার জন্য প্রতিটি ভেরিয়েবলের মান প্রদান করতে চাই। আমরা যে গ্রাফটি তৈরি করি তার শীর্ষবিন্দুগুলির একটি টপোলজিকাল বাছাইয়ের সাথে এটি সম্পাদন করা যেতে পারে। টপোলজিক্যাল সাজানোর ক্ষেত্রে xi-এর পরে xi থাকলে, xi-কে মিথ্যা হিসাবে গণ্য করা উচিত। অন্যথায় এটি সত্য হিসাবে বিবেচিত হওয়া উচিত।
ছদ্ম কোড
func dfsFirst1(vertex v1): marked1[v1] = true for each vertex u1 adjacent to v1 do: if not marked1[u1]: dfsFirst1(u1) stack.push(v1) func dfsSecond1(vertex v1): marked1[v1] = true for each vertex u1 adjacent to v1 do: if not marked1[u1]: dfsSecond1(u1) component1[v1] = counter for i = 1 to n1 do: addEdge1(not x[i], y[i]) addEdge1(not y[i], x[i]) for i = 1 to n1 do: if not marked1[x[i]]: dfsFirst1(x[i]) if not marked1[y[i]]: dfsFirst1(y[i]) if not marked1[not x[i]]: dfsFirst1(not x[i]) if not marked1[not y[i]]: dfsFirst1(not y[i]) set all marked values false counter = 0 flip directions of edges // change v1 -> u1 to u1 -> v1 while stack is not empty do: v1 = stack.pop if not marked1[v1] counter = counter + 1 dfsSecond1(v1) for i = 1 to n1 do: if component1[x[i]] == component1[not x[i]]: it is unsatisfiable exit if component1[y[i]] == component1[not y[i]]: it is unsatisfiable exit it is satisfiable exit


