বাইনোমিয়াল হিপকে বাইনারি হিপের একটি এক্সটেনশন হিসাবে সংজ্ঞায়িত করা হয় যা বাইনারি হিপ দ্বারা প্রদত্ত অন্যান্য ক্রিয়াকলাপগুলির সাথে একত্রে দ্রুত একত্রিতকরণ বা একত্রিতকরণ প্রদান করে৷
দ্বিপদ স্তূপকে দ্বিপদী গাছের সংগ্রহ হিসাবে বিবেচনা করা হয়।
দ্বিপদী গাছ কি?
K-1 অর্ডারের দুটি দ্বিপদী গাছ নিয়ে এবং একটিকে বামদিকের শিশু বা অন্যটিকে বিবেচনা করে একটি দ্বিপদ গাছ তৈরি করা যেতে পারে।
একটি দ্বিপদী গাছের ক্রম k নীচের বৈশিষ্ট্য রয়েছে৷
-
দ্বিপদ গাছের নোডের সংখ্যা ঠিক 2 k .
-
দ্বিপদী গাছের গভীরতা হল k.
-
গভীরতায় ঠিক kCi নোড আছে i যেখানে i =0, 1, . . . , k.
-
ডিগ্রী k সহ মূল এবং মূলের সন্তানগুলিকে k-1, k-2,..0 ক্রম সহ বাম থেকে ডানে দ্বিপদ গাছ হিসাবে গণ্য করা হয়।
দ্বিপদ স্তূপ −
একটি দ্বিপদ স্তূপকে দ্বিপদ গাছের একটি সেট হিসাবে সংজ্ঞায়িত করা হয় যেখানে প্রতিটি দ্বিপদী গাছ MinHeap সম্পত্তি অনুসরণ করে। এবং যেকোনো ডিগ্রি থাকলে, যেকোনো ডিগ্রির সর্বোচ্চ একটি দ্বিপদী বৃক্ষ থাকতে পারে।
উদাহরণ দ্বিপদী হিপ −
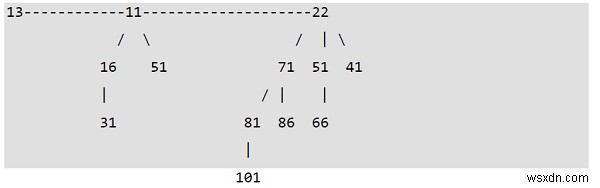
12টি নোড বিশিষ্ট একটি দ্বিপদ স্তূপ। এটিকে 2
এর সংগ্রহ হিসাবে বিবেচনা করা হয়বাম থেকে ডানে দ্বিপদী বৃক্ষের অর্ডার 2 এবং 3

দ্বিপদ স্তূপ এবং একটি সংখ্যার বাইনারি প্রতিনিধিত্ব
m নোড সম্বলিত একটি দ্বিপদ স্তূপের মধ্যে দ্বিপদ গাছের সংখ্যা m-এর বাইনারি উপস্থাপনায় সেট বিটের সংখ্যার সমান। উদাহরণস্বরূপ, ধরুন m 13, m (00001101) এর বাইনারি উপস্থাপনায় 3 সেট বিট রয়েছে, যা 3টি দ্বিপদী গাছ নির্দেশ করে। আমরা সেট বিটের অবস্থানের সাথে এই দ্বিপদী গাছের ডিগ্রির সাথে সম্পর্ক স্থাপন করতেও সক্ষম হতে পারি। এই সম্পর্কের সাহায্যে, আমরা সিদ্ধান্ত নিতে পারি বা উপসংহারে আসতে পারি যে 'm' নোড সহ একটি BinomialHeap-এ O(logm) দ্বিপদী গাছ রয়েছে
দ্বিপদ স্তূপের ক্রিয়াকলাপ -
union() হল বাইনোমিয়াল হিপের প্রধান অপারেশন, অন্যান্য সমস্ত অপারেশন প্রধানত এই অপারেশনটি বাস্তবায়ন করে। ইউনিয়ন() অপারেশন দুটি দ্বিপদী হিপকে একত্রিত করার জন্য দায়ী।
-
সন্নিবেশ(h, K)− দ্বিপদী হিপ 'h'-এ একটি কী 'K' সন্নিবেশ করায়। প্রথমে, এই অপারেশনটি একক কী 'K' সহ একটি দ্বিপদী হিপ তৈরি করতে সক্ষম হয়, তারপরে h এবং নতুন দ্বিপদী হিপকে কল করে।
-
getMin(h)− getMin() করার একটি সহজ পদ্ধতি হল দ্বিপদী গাছের মূল তালিকা পরিদর্শন করা এবং সবচেয়ে ছোট কী ফেরত দেওয়া।
এই অ্যাপ্লিকেশনটির জন্য O(logm) সময় প্রয়োজন। একটি পয়েন্টারটো ক্ষুদ্রতম কী রুট বজায় রেখে এটিকে O(1) এ উন্নত করা যেতে পারে।
-
extractMin(h)− এই অপারেশনটি ইউনিয়ন() প্রয়োগ করে। প্রথমে, আমরা getMin() কল করি ক্ষুদ্রতম কী দ্বিপদী ট্রি গণনা করার জন্য, তারপরে আমরা নোডটি সরিয়ে ফেলি এবং সরানো ক্ষুদ্রতম নোডের সমস্ত সাবট্রি একত্রিত করে একটি নতুন দ্বিপদী হিপ তৈরি করি। সবশেষে, আমরা কলউনিয়ন() তে h এর পাশাপাশি সদ্য নির্মিত দ্বিপদী হিপ। এই অপারেশনের জন্য O(logm)সময় প্রয়োজন।
-
ডিলিট(h)− বাইনারি হিপের মতোই, প্রথমে, ডিলিট অপারেশন কী কমিয়ে দেয় minusinfinite, পরবর্তী কলগুলি extractMin()।
-
reduceKey(h)− reduceKey() বাইনারি হিপের মতোই। প্রথমে, আমরা এটির সাথে পিতামাতার সাথে হ্রাসকৃত কী তুলনা করি এবং যদি পিতামাতার কীটি বেশি হয়, তাহলে আমরা কীগুলি বিনিময় করি এবং পিতামাতার জন্য পুনরাবৃত্তি করি। শেষ অবধি, আমরা থামি যখন আমরা হয় একটি নোডে পৌঁছাই যার প্যারেন্টের একটি ছোট কী আছে বা আমরা রুট নোডে পৌঁছাই। reduceKey() এর সময় জটিলতা হল O(logm)।


