এই সমস্যায়, আমাদেরকে একটি বাইনারি গাছের ইনঅর্ডার এবং পোস্টঅর্ডার ট্রাভার্সাল দেওয়া হয়েছে। আমাদের কাজ হল গাছের পোস্টঅর্ডার ট্রাভার্সাল প্রিন্ট করা।
সমস্যাটি বোঝার জন্য একটি উদাহরণ নেওয়া যাক
Input:inorder: 16 7 21 12 1 5 9 postorder: 16 21 7 1 9 5 12 Output: preorder: 12 7 16 21 5 1 9 Explanation: the binary tree is :
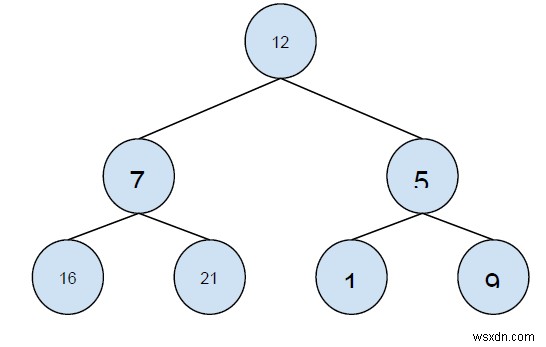
এই সমস্যাটি সমাধান করার জন্য, একটি সহজ সমাধান হল প্রদত্ত ট্রাভার্সালগুলি ব্যবহার করে একটি গাছ তৈরি করা এবং তারপর গাছের প্রি-অর্ডার ট্রাভার্সাল খুঁজে বের করা। কিন্তু এই পদ্ধতিটি সিস্টেমের জন্য আরও জটিল হবে৷
৷সমস্যা সমাধানের জন্য আরও কার্যকরী সমাধান হল স্ট্যাক ডেটা স্ট্রাকচার ব্যবহার করা। আসুন গাছের প্রতিটি নোড দেখি। পোস্টঅর্ডার ট্রাভার্সালের শেষ আইটেম হল গাছের মূল। এখন আমাদের বাইনারি গাছের বাম এবং ডান সাবট্রি আলাদা করতে হবে। যেহেতু আমরা গাছের রুট নোড জানি। পোস্টঅর্ডার ট্রাভার্সালে, রুট নোডের আগে সমস্ত উপাদান বাম সাবট্রির এবং রুটের পরে ডান সাবট্রির।
এইভাবে, আমরা সমস্ত উপাদান খুঁজে পাব এবং স্ট্যাকের মধ্যে নোডগুলি সংরক্ষণ করব এবং স্ট্যাকের প্রিন্ট উপাদানগুলি যা প্রি-অর্ডার ট্রাভার্সাল দেয়৷
জাভাতে আমাদের সমাধানের বাস্তবায়ন
উদাহরণ
import java.util.Stack;
public class Main {
static int postIndex;
void preOrder(int[] in, int[] post, int inStrt, int inEnd, Stack<Integer> preorder) {
if (inStrt > inEnd)
return;
int val = post[postIndex];
int inIndex = searchValue(in, val);
postIndex--;
preOrder(in, post, inIndex + 1, inEnd, preorder);
preOrder(in, post, inStrt, inIndex - 1, preorder);
preorder.push(val);
}
void printPreOrderTraversal(int[] in, int[] post) {
int len = in.length;
postIndex = len - 1;
Stack<Integer> preorder = new Stack<Integer>();
preOrder(in, post, 0, len - 1, preorder);
while (preorder.empty() == false)
System.out.print(preorder.pop()+" ");
}
int searchValue(int[] in, int data){
int i = 0;
for (i = 0; i < in.length; i++)
if (in[i] == data)
return i;
return i;
}
public static void main(String ars[]){
int in[] = { 4, 10, 12, 15, 18, 22, 24, 25, 31, 35, 44, 50, 66, 70, 90 };
int post[] = { 4, 12, 10, 18, 24, 22, 15, 31, 44, 35, 66, 90, 70, 50, 25 };
Main tree = new Main();
System.out.println("Preorder Traversal of the tree is: ");
tree.printPreOrderTraversal(in, post);
}
} আউটপুট
Preorder Traversal of the tree is: 25 15 10 4 12 22 18 24 50 35 31 44 70 66 90


