C++ এ ট্রি নোড মুছুন

ধরুন আমাদের একটি গাছ আছে, এই গাছটি নোড 0 এ রুট করা হয়েছে, এটি নিম্নরূপ দেওয়া হল -

1. নোডের সংখ্যা হল নোড
2. ith নোডের মান হল মান[i]
3. ith নোডের প্যারেন্ট হল প্যারেন্ট[i]

আমাদের প্রত্যেকটি সাবট্রি মুছে ফেলতে হবে যার নোডের মানের সমষ্টি 0, এটি করার পরে গাছে অবশিষ্ট নোডের সংখ্যা ফেরত দিতে হবে। তাই গাছটি যদি −

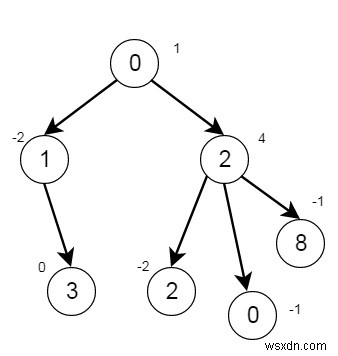
7টি নোড আছে, আউটপুট হবে 2

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• শিশু নামে একটি মানচিত্র তৈরি করুন
• dfs() নামে একটি পদ্ধতি সংজ্ঞায়িত করুন, এটি নোড, একটি অ্যারের মান এবং গ্রাফ গ্রহণ করবে
• temp :=একটি জোড়া (মান [নোড], 1)
• আমি 0 থেকে গ্রাফের আকার [নোড]
  পরিসরে
  • temp2 :=dfs(গ্রাফ[নোড, i], মান, গ্রাফ)
  • টেম্প২-এর প্রথম দিয়ে প্রথম বাড়ান, টেম্প২-এর দ্বিতীয় দিয়ে দ্বিতীয় বাড়ান
• যদি temp এর প্রথমটি 0 হয়, তাহলে ans :=ans – temp এর সেকেন্ড, temp এর সেকেন্ড সেট করুন :=0
• রিটার্ন টেম্প
• প্রধান পদ্ধতি থেকে, এটি নোড, পিতামাতার অ্যারে এবং মান অ্যারে নেবে
• n :=মান অ্যারেতে উপস্থিত মানের সংখ্যা
• উত্তর :=n
• n + 1 আকারের একটি অ্যারে গ্রাফ সংজ্ঞায়িত করুন
• আমি 1 থেকে n – 1
  পরিসরে
  • গ্রাফে আমি সন্নিবেশ করান[পিতা[i]]
• dfs(0, মান, গ্রাফ)
• উত্তর ফেরত দিন

উদাহরণ(C++)

আরো ভালোভাবে বোঝার জন্য নিচের বাস্তবায়নটি দেখি -

#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
   map <int, int> children;
   int ans;
   pair <int, int> dfs(int node, vector<int>& value, vector <int> graph[]){
      pair <int, int> temp = {value[node], 1};
      for(int i = 0; i < graph[node].size(); i++){
         pair <int, int> temp2 = dfs(graph[node][i], value, graph);
         temp.first += temp2.first;
         temp.second += temp2.second;
      }
      if(temp.first == 0){
         ans -= temp.second;
         temp.second = 0;
      }
      return temp;
   }
   int deleteTreeNodes(int nodes, vector<int>& parent, vector<int>& value) {
      int n = value.size();
      ans = n;
      children.clear();
      vector < int > graph[n + 1];
      for(int i = 1; i < n; i++){
         graph[parent[i]].push_back(i);
      }
      dfs(0, value, graph);
      return ans;
   }
};
main(){
   vector<int> v1 = {-1,0,0,1,2,2,2};
   vector<int> v2 = {1,-2,4,0,-2,-1,-1};
   Solution ob;
   cout << (ob.deleteTreeNodes(7,v1, v2));
}

ইনপুট

7
[-1,0,0,1,2,2,2]
[1,-2,4,0,-2,-1,-1]

আউটপুট

2