শিরোনাম হিসাবে একটি গাছের নোড ধারণকারী একটি অনির্দেশিত গ্রাফ দেওয়া হয়েছে। লক্ষ্য হল BFS( ব্রেডথ ফার্স্ট সার্চ ) অ্যালগরিদম ব্যবহার করে গাছের একটি প্রদত্ত স্তরে নোডের গণনা খুঁজে বের করা।
BFS অ্যালগরিদম:-
এই অ্যালগরিদমটি গ্রাফ/ট্রি লেভেলকে লেভেলে ট্র্যাভার্স করা শুরু করে। লেভেল 0 এ নোড থেকে শুরু করে, এটি প্রথমে লেভেল 1 এ এটির সাথে সরাসরি সংযুক্ত সমস্ত নোড অতিক্রম করবে, তারপর পরবর্তী লেভেলে সমস্ত নোড অতিক্রম করবে ইত্যাদি৷
- বর্তমান স্তরে অনুভূমিকভাবে নোডগুলি অতিক্রম করুন৷
- একই পদ্ধতিতে পরবর্তী স্তরে নোডগুলি অতিক্রম করুন৷ ৷
আসুন উদাহরণ দিয়ে বোঝা যাক।
উদাহরণস্বরূপ
ইনপুট - স্তর=2

আউটপুট - BFS ব্যবহার করে একটি গাছে প্রদত্ত স্তরে নোডের সংখ্যা হল:1
ব্যাখ্যা - উপরে দেখানো হিসাবে সমস্ত স্তরের গ্রাফে একটি একক নোড রয়েছে।
ইনপুট - স্তর=1
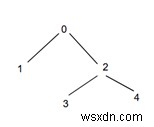
আউটপুট - BFS ব্যবহার করে একটি গাছে প্রদত্ত স্তরে নোডের সংখ্যা হল:2
ব্যাখ্যা - উপরে দেখানো হিসাবে সমস্ত স্তরের গ্রাফে একটি একক নোড রয়েছে। নোডগুলি হল 1, 2।
নিম্নলিখিত প্রোগ্রামে ব্যবহৃত পদ্ধতি
এই পদ্ধতিতে আমরা প্রতিটি নোড অতিক্রম করব এবং তাদের স্তরগুলিকে তার অভিভাবকের চেয়ে এক স্তর বেশি হিসাবে সেট করব। আমরা সংলগ্ন তালিকা উপস্থাপনা ব্যবহার করে একটি গ্রাফ উপস্থাপন করব।
যদি স্টার্টিং নোড 0 হয় তাহলে
স্তর[0]=0,
লেভেল[1] =লেভেল[0]+1 =1, লেভেল[2]=লেভেল[0]+1=1
লেভেল[3]=লেভেল[2]+1 =2, লেভেল[4]=লেভেল[2]+1=2

- একটি শ্রেণী নোড তৈরি করুন যা একটি গ্রাফ উপস্থাপন করে শীর্ষবিন্দুর সংখ্যা হিসাবে এবং পাশের সংলগ্ন তালিকার পয়েন্টার হিসাবে।
- পাবলিক পদ্ধতি সন্নিবেশ (int val, int পয়েন্ট) গ্রাফে প্রান্ত যোগ করে।
- এটি পয়েন্টের সংলগ্ন তালিকায় val যোগ করে এবং val-এর সংলগ্ন তালিকায় নির্দেশ করে৷
- ফাংশন count_nodes(int a, int b) সোর্স নোড a থেকে শুরু করে B স্তরে নোডের গণনা প্রদান করে।
- প্রাথমিক গণনা 0 হিসাবে সেট করুন।
- বুল অ্যারে চেক নিন =নতুন বুল[ডেটা]।
- অ্যারে অ্যারে[ডেটা] গ্রাফের প্রতিটি শীর্ষবিন্দুর স্তর সংরক্ষণ করে।
- লুপ এবং সেট চেক[i] =মিথ্যা এবং arr[i] =0 ব্যবহার করে গ্রাফের সমস্ত শীর্ষকে অ-ভিজিট হিসাবে সেট করুন।
- BFS ট্রাভার্সালের জন্য একটি সারি l1 তৈরি করুন।
- চেক[a] =সত্য হিসাবে পরিদর্শন করা শুরুর শীর্ষকে চিহ্নিত করুন এবং l1.push_back(a) ব্যবহার করে এটিকে l1 এ যোগ করুন এবং এর স্তর 0. arr[a] =0 হিসাবে সেট করুন।
- যদিও সারি l1 অ-খালি।
- সামনের উপাদানটিকে a =l1 হিসাবে নিন। front() এবং l1.pop_front(). ব্যবহার করে প্রিন্ট করুন
- a এর সমস্ত সংলগ্ন অপ্রদর্শিত শীর্ষগুলিকে পরিদর্শন হিসাবে চিহ্নিত করুন এবং সারিতে l1 যোগ করুন৷
- প্রতিটি সন্নিহিত শীর্ষবিন্দুর স্তর a + 1 এর স্তর হিসাবে সেট করুন।
- হোয়্যাল লুপের শেষে ট্রাভার্স arr[] লুপ ব্যবহার করে এবং প্রতিটি arr এর জন্য [i] ==b ইনক্রিমেন্ট কাউন্ট।
- শেষে ফলাফল হিসাবে ফেরত গণনা,
উদাহরণ
#include <bits/stdc++.h>
using namespace std;
class node {
int data;
list < int > * next;
public:
node(int data) {
this -> data = data;
next = new list < int > [data];
}
void insert(int val, int point) {
next[val].push_back(point);
next[point].push_back(val);
}
int count_nodes(int a, int b);
};
int node::count_nodes(int a, int b) {
int count = 0;
bool * check = new bool[data];
int arr[data];
for (int i = 0; i < data; i++) {
check[i] = false;
arr[i] = 0;
}
list < int > l1;
check[a] = true;
l1.push_back(a);
arr[a] = 0;
while (!l1.empty()) {
a = l1.front();
l1.pop_front();
for (auto it = next[a].begin(); it != next[a].end(); ++it) {
if (!check[ * it]) {
arr[ * it] = arr[a] + 1;
check[ * it] = true;
l1.push_back( * it);
}
}
}
for (int i = 0; i < data; i++) {
if (arr[i] == b) {
count++;
}
}
return count;
}
int main() {
node n1(5);
n1.insert(1, 2);
n1.insert(0, 3);
n1.insert(1, 3);
n1.insert(2, 4);
int level = 1;
cout << "Count of number of nodes at given level in a tree using BFS are: " << n1.count_nodes(0, level);
return 0;
} যদি আমরা উপরের কোডটি চালাই তবে এটি নিম্নলিখিত আউটপুট −
উৎপন্ন করবেআউটপুট
Count of number of nodes at given level in a tree using BFS are: 1


