বৃত্তাকার অ্যারেতে সর্বাধিক যোগফল যাতে C++ এ দুটি উপাদান সংলগ্ন থাকে না

এই সমস্যায়, আমাদের একটি বৃত্তাকার অ্যারে দেওয়া হয়েছে cirArr[]। আমাদের কাজ হল সার্কুলার অ্যারেতে সর্বাধিক যোগফল খুঁজে বের করার জন্য একটি প্রোগ্রাম তৈরি করা যাতে C++ এ দুটি উপাদান সংলগ্ন না থাকে।

সমস্যা বর্ণনা

বৃত্তাকার অ্যারের জন্য, আমাদের অ্যারের উপাদানগুলির সর্বাধিক যোগফল খুঁজে বের করতে হবে যাতে সংলগ্ন উপাদানগুলি নেওয়া যায় না অর্থাৎ আমাদের বিকল্প উপাদানগুলি নিতে হবে৷

বৃত্তাকার অ্যারে একটি বিশেষ ধরনের অ্যারে যেখানে অ্যারের শেষ উপাদানটি প্রথম উপাদানের সাথে সংযুক্ত থাকে৷

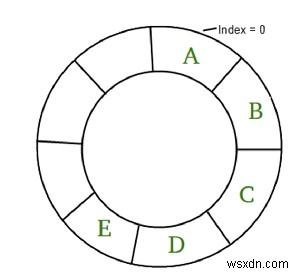
সমস্যাটি বোঝার জন্য একটি উদাহরণ নেওয়া যাক,

ইনপুট

cirArr[] = {4, 1, 5, 3, 2}

আউটপুট

9

ব্যাখ্যা

সর্বাধিক যোগফল বৃত্তাকার অনুগামী হল [4, 5, 2]। যোগফল =9

সমাধান পদ্ধতি

সমস্যার সমাধান হল সর্বাধিক যোগফল খুঁজে পেতে একটি গতিশীল প্রোগ্রামিং পদ্ধতি ব্যবহার করা। বৃত্তাকার অ্যারেটিকে দুটি অ্যারে হিসাবে বিবেচনা করে যোগফল বের করা যেতে পারে, একটি সূচক 0 থেকে N-2 এবং অন্যটি সূচক 1 থেকে n-1 পর্যন্ত। এটি দুটি অ্যারে তৈরি করবে এবং এই অ্যারের থেকে সর্বাধিক যোগফলের যোগফল হবে৷

উদাহরণ

আমাদের সমাধানের কাজ চিত্রিত করার জন্য প্রোগ্রাম,

#include <iostream>
using namespace std;
int calcMaxVal(int a, int b){
   if(a > b)
      return a;
   return b;
}
int calcMaxSumSubSeq(int cirArr[], int start, int end, int n) {
   int DP[n];
   int maxSum = 0;
   for (int i = start; i < (end + 1); i++) {
      DP[i] = cirArr[i];
      if (maxSum < cirArr[i])
         maxSum = cirArr[i];
   }
   for (int i = (start + 2); i < (end + 1); i++) {
      for (int j = 0; j < i - 1; j++) {
         if (DP[i] < DP[j] + cirArr[i]) {
            DP[i] = DP[j] + cirArr[i];
            if (maxSum < DP[i])
               maxSum = DP[i];
         }
      }
   }
   return maxSum;
}
int findMaxSum(int cirArr[], int n){
   int maxSumArray1 = calcMaxSumSubSeq(cirArr, 0, (n-2), n);
   int maxSumArray2 = calcMaxSumSubSeq(cirArr, 1, (n-1), n);
   int maxSum = calcMaxVal(maxSumArray1, maxSumArray2);
   return maxSum;
}
int main(){
   int cirArr[] = {4, 1, 5, 3, 2};
   int n = sizeof(cirArr)/sizeof(cirArr[0]);
   cout<<"The maximum sum in circular array such that no two elements are adjacent is "<<findMaxSum(cirArr, n);
   return 0;
}

আউটপুট

The maximum sum in circular array such that no two elements are adjacent is 9