এই সমস্যায়, আমাদের প্রতিটি নোডের একটি মান সহ একটি বাইনারি ট্রি দেওয়া হয়েছে৷ আমাদের কাজ হল বাইনারিট্রিতে নোডের সর্বাধিক যোগফল খুঁজে বের করার জন্য একটি প্রোগ্রাম তৈরি করা যাতে দুটি সংলগ্ন না হয়। ডায়নামিক প্রোগ্রামিং ব্যবহার করে।
সমস্যা বর্ণনা − আমরা বাইনারি গাছের উপসেটগুলি বেছে নেব যাতে যোগফল সর্বাধিক করা যায় যাতে নোডগুলি সরাসরি সংযুক্ত না হয়৷
সমস্যাটি বোঝার জন্য একটি উদাহরণ নেওয়া যাক,
ইনপুট
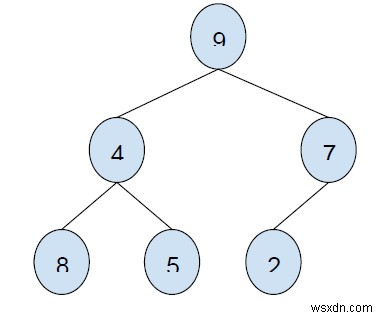
আউটপুট
24
ব্যাখ্যা
Elements to be taken under consideration are: 8 + 5 + 9 + 2 = 24
সমাধান পদ্ধতি
সমস্যার সমাধান হল একটি মানচিত্র ব্যবহার করে এবং নোডের যোগফল খুঁজে বের করা যা তারা maxSum গঠন করে। নোড এবং তাদের সন্তান উভয়ই হতে পারে না
প্রদত্ত শর্ত অনুযায়ী যোগফলের জন্য বিবেচনা করা হয়। সুতরাং, আমাদের এই সত্যটি পরীক্ষা করতে হবে যে একটি নোড বিবেচনা করার আগে, আমাদের চেক করতে হবে যে এর চাইল্ডট্রিতে এমন কিছু উপাদান আছে যা একটি বড় যোগফল গঠন করে।
প্রতিটি নোডের জন্য একই পিতা-মাতা-শিশু সাবট্রির যোগফল একাধিকবার খুঁজে বের করলে গণনার ওভারহেড বাড়বে এবং এটি মোকাবেলা করার জন্য, আমরা মুখস্থ ব্যবহার করব এবং ম্যাক্সসুমকে একটি মানচিত্রে নোড পর্যন্ত সংরক্ষণ করব যা পরে ব্যবহার করা যেতে পারে।
উদাহরণ
আমাদের সমাধানের কাজ চিত্রিত করার জন্য প্রোগ্রাম,
#include <bits/stdc++.h>
using namespace std;
struct node{
int data;
struct node *left, *right;
};
struct node* newNode(int data){
struct node *temp = new struct node;
temp−>data = data;
temp−>left = temp−>right = NULL;
return temp;
}
int findMaxSumBT(node* node, map<struct node*, int>& nodeSum);
int sumSubTreeNodes(node* node, map<struct node*, int>& nodeSum){
int maxSum = 0;
if (node−>left)
maxSum += findMaxSumBT(node−>left−>left, nodeSum) +
findMaxSumBT(node−>left−>right, nodeSum);
if (node−>right)
maxSum += findMaxSumBT(node−>right−>left, nodeSum) +
findMaxSumBT(node−>right−>right, nodeSum);
return maxSum;
}
int findMaxSumBT(node* node, map<struct node*, int>& nodeSum){
if (node == NULL)
return 0;
if (nodeSum.find(node) != nodeSum.end())
return nodeSum[node];
int sumInclCurr = node−>data + sumSubTreeNodes(node, nodeSum);
int sumExclCurr = findMaxSumBT(node−>left, nodeSum) +
findMaxSumBT(node−>right, nodeSum);
nodeSum[node] = max(sumInclCurr, sumExclCurr);
return nodeSum[node];
}
int main(){
node* root = newNode(9);
root−>left = newNode(4);
root−>right = newNode(7);
root−>left−>left = newNode(8);
root−>left−>right = newNode(5);
root−>right−>left = newNode(2);
map<struct node*, int> nodeSum;
cout<<"Maximum sum of nodes in Binary tree such that no two are
adjacent using Dynamic Programming is "<<findMaxSumBT(root,
nodeSum);
return 0;
} আউটপুট
Maximum sum of nodes in Binary tree such that no two are adjacent using Dynamic Programming is 24


