ধারণা
ধরুন p এবং প্রস্থ q দৈর্ঘ্যের একটি বোর্ড দেওয়া আছে, আমাদের এই বোর্ডটিকে p*q স্কোয়ারে ভাঙ্গতে হবে যাতে ভাঙার খরচ কম হয়। এই বোর্ডের জন্য, প্রতিটি প্রান্তের জন্য কাটিয়া খরচ দেওয়া হবে। সংক্ষেপে, আমাদের এমন একটি ক্রম নির্বাচন করতে হবে যাতে খরচ কম হয়।
উদাহরণ
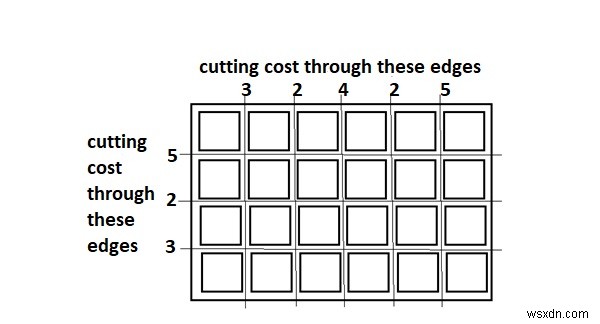
উপরের বোর্ডের ক্ষেত্রে বর্গাকারে কাটার সর্বোত্তম উপায় হল −
উপরোক্ত ক্ষেত্রে মোট সর্বনিম্ন খরচ হল 65। এটি নিম্নলিখিত পদক্ষেপগুলি বাস্তবায়ন করে গণনা করা হয়।
Initial Value : Total_cost = 0 Total_cost = Total_cost + edge_cost * total_pieces Cost 5 Horizontal cut Cost = 0 + 5*1 = 5 Cost 5 Vertical cut Cost = 5 + 5*2 = 15 Cost 4 Vertical cut Cost = 15 + 4*2 = 23 Cost 3 Horizontal cut Cost = 23 + 3*3 = 32 Cost 3 Vertical cut Cost = 32 + 3*3 = 41 Cost 2 Horizontal cut Cost = 41 + 2*4 = 49 Cost 2 Vertical cut Cost = 49 + 2*4 = 57 Cost 2 Vertical cut Cost = 57 + 2*4 = 65
পদ্ধতি
লোভী পন্থা প্রয়োগ করে এই ধরনের সমস্যা সমাধান করা যেতে পারে। যদি মোট খরচকে S দ্বারা গণ্য করা হয়, তাহলে S =b1x1 + b2x2 … + bkxk, যেখানে xi নির্দিষ্ট প্রান্ত কাটার খরচ হিসাবে ধরা হয় এবং bi অনুরূপ সহগ, সহগ bi নির্ধারণ করা হয় আমরা যে সমস্ত কাটের মোট সংখ্যার দ্বারা আমরা প্রতিযোগিতা করেছি কাটা প্রক্রিয়া শেষে xi।
আমাদের লক্ষ্য করা উচিত যে সহগগুলির যোগফল সর্বদা ধ্রুবক থাকে, তাই আমরা দ্বি-প্রাপ্তির একটি বন্টন গণনা করতে চাই যাতে S সর্বনিম্ন হয়। এটি করার জন্য আমরা যত তাড়াতাড়ি সম্ভব সবচেয়ে বড় খরচের প্রান্তে কাটগুলি সম্পন্ন করি, যা সর্বোত্তম S-এ পৌঁছাবে৷ যদি আমরা সমান খরচের বেশ কয়েকটি প্রান্তের সম্মুখীন হই, তাহলে আমরা প্রথমে তাদের যেকোনো একটিকে সরিয়ে ফেলতে বা কাটতে পারি৷
C++ প্রোগ্রাম
উপরের পদ্ধতির বাস্তবায়নের সমাধানটি নিচে দেওয়া হল, প্রথমে আমরা বিপরীত ক্রমে প্রান্ত কাটানোর খরচগুলি সাজিয়েছি, এবং তারপর আমরা আমাদের সমাধান তৈরি করতে উচ্চ খরচ থেকে কম খরচে সেগুলি লুপ করি। যতবার আমরা একটি প্রান্ত নির্বাচন করি, প্রতিবার কাউন্টারপার্টের সংখ্যা 1 দ্বারা বৃদ্ধি পায়, যা প্রতিবার সংশ্লিষ্ট প্রান্ত কাটানোর খরচের সাথে গুণ করতে হবে।
উদাহরণ
// C++ program to divide a board into p*q squares
#include <bits/stdc++.h>
using namespace std;
int minimumCostOfBreaking(int X1[], int Y1[], int p, int q){
int res1 = 0;
sort(X1, X1 + p, greater<int>());
sort(Y1, Y1 + q, greater<int>());
int hzntl = 1, vert = 1;
int i = 0, j = 0;
while (i < p && j < q){
if (X1[i] > Y1[j]){
res1 += X1[i] * vert;
hzntl++;
i++;
}
else{
res1 += Y1[j] * hzntl;
vert++;
j++;
}
}
int total = 0;
while (i < p)
total += X1[i++];
res1 += total * vert;
total = 0;
while (j < q)
total += Y1[j++];
res1 += total * hzntl;
return res1;
}
int main(){
int p = 6, q = 4;
int X1[p-1] = {3, 2, 4, 2, 5};
int Y1[q-1] = {5, 2, 3};
cout << minimumCostOfBreaking(X1, Y1, p-1, q-1);
return 0;
} আউটপুট
65


