আমাদের একটি ইনপুট N দেওয়া হয়েছে যা দাবাবোর্ডের আকার নির্দেশ করে। এখানে কাজটি হল N-এর কোন মান খুঁজে বের করা, NXN চেসবোর্ডে কতগুলি বিশপ স্থাপন করা যেতে পারে যাতে কোনও দুই বিশপ একে অপরকে আক্রমণ করতে না পারে। উদাহরণ দিয়ে বোঝা যাক।
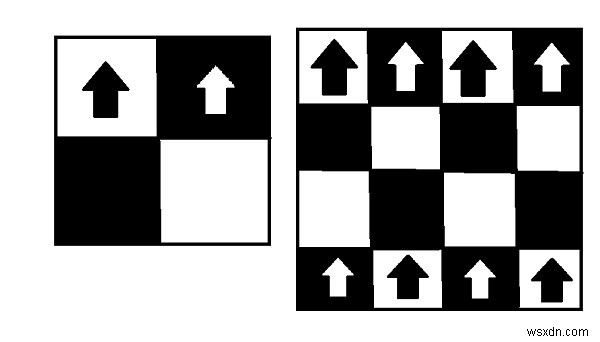
ইনপুট − N=2
আউটপুট − সর্বাধিক বিশপ যা N*N চেসবোর্ডে স্থাপন করা যেতে পারে − 2 (উপরে দেখানো হয়েছে)
ব্যাখ্যা − যেমন উপরে চিত্রিত করা হয়েছে শুধুমাত্র অ-বিরোধী অবস্থানগুলি যেখানে বিশপদের স্থাপন করা হয়েছে। 2X2 চেসবোর্ডের জন্য সর্বাধিক বিশপ।
ইনপুট − N=5
আউটপুট − সর্বাধিক বিশপ যা N*N চেসবোর্ডে স্থাপন করা যেতে পারে:8 (উপরে দেখানো হয়েছে)
নিম্নলিখিত প্রোগ্রামে ব্যবহৃত পদ্ধতি
-
আমরা দাবাবোর্ডের মাত্রার জন্য ইনপুট হিসাবে একটি পূর্ণসংখ্যার মান N নিই।
-
টোটালবিশপস(int n) কে যুক্তি হিসাবে এই এনটি পাস করুন।
-
N<1 অবৈধ ইনপুটের জন্য, বিশপ গণনা=0।
-
N=1 এর জন্য, শুধুমাত্র 1 পজিশন, বিশপ কাউন্ট=1।
-
অন্য বিশপ হবেন 2*(N-1)
-
এই ফলাফলটি পরিবর্তনশীল বিশপে সংরক্ষণ করুন।
-
ফলাফল ফেরত দিন।
উদাহরণ
#include <iostream>
//to return maximum bishops possible
int totalBishops(int n){
int bishops=0;
if (n < 1)
bishops= 0;
else if (n == 1)
bishops= 1;
else
bishops= 2 * (n - 1);
return bishops;
}
int main(){
int N = 15; //for chessboard dimensions N*N
printf("%d" ,totalBishops(N));
return 0;
} আউটপুট
যদি আমরা উপরের কোডটি চালাই তবে এটি নিম্নলিখিত আউটপুট −
উৎপন্ন করবে28


