এই সমস্যায়, আমাদের একটি সম্পূর্ণ বাইনারি গাছ দেওয়া হয়। আমাদের কাজ হল একটি সম্পূর্ণ বাইনারি গাছের মিরর ইমেজ নোডের যোগফলকে একটি ক্রমানুসারে খুঁজে বের করার জন্য একটি প্রোগ্রাম তৈরি করা৷
এখানে, আমাদের বাম সূর্য-বৃক্ষের অভ্যন্তরীণ ট্রাভার্সাল খুঁজে বের করতে হবে, এবং তারপর প্রতিটি নোডের জন্য, আমরা এর সাথে মিরর ইমেজ যোগ করব। এর অর্থ হল যদি আমরা বাম পাতার নোডটি অতিক্রম করি, আমরা এটির সাথে ডান পাতার নোডের মান যোগ করব। যেহেতু এটি মিরর ইমেজ নোড।
কিছু গুরুত্বপূর্ণ সংজ্ঞা
সম্পূর্ণ বাইনারি ট্রি একটি বাইনারি ট্রি যেখানে শেষ স্তর ছাড়া সব স্তরেই সর্বাধিক সংখ্যক নোড থাকে৷
অভ্যন্তরীণ ট্রাভার্সাল একটি ট্রি ট্রাভার্সাল কৌশল যেখানে প্রথমে বাম সাবট্রি পরিদর্শন করা হয়, মূলটি পরিদর্শন করা হয় এবং ডান সাব-ট্রি পরিদর্শন করা হয়।
সমস্যাটি বোঝার জন্য একটি উদাহরণ নেওয়া যাক,
ইনপুট
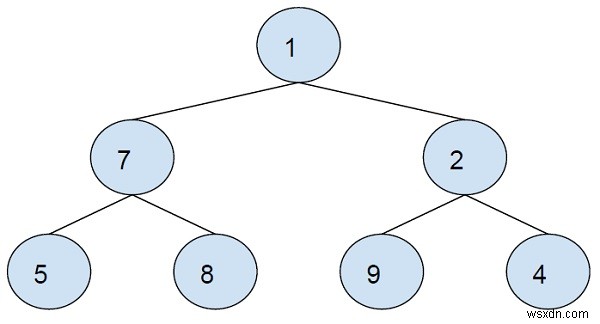
আউটপুট − 9 9 17 2
ব্যাখ্যা − বাম সাবট্রির ইনঅর্ডার ট্রাভার্সাল হল 5-7-8-1।
সমস্ত নোড যোগ করা ছবিগুলিকে মিরর করবে৷
৷5 + 4 = 9 7 + 2 = 9 8 + 9 = 17 1 + 1 = 2
এই সমস্যাটি সমাধান করার জন্য, আমরা ইনঅর্ডার ট্রাভার্সাল ব্যবহার করে বাইনারি ট্রিটি অতিক্রম করব। আমরা দুটি নোড ব্যবহার করব, একটি বাম সাবট্রি অতিক্রম করতে এবং অন্যটি নোডের আয়না দেখার জন্য। উদাহরণস্বরূপ, আমাদের বাম সাবট্রির জন্য একটি রুট নোড আছে এবং এর জন্য আমাদের কাছে মিরররুট থাকবে যা এটির মিরর ইমেজকে অতিক্রম করবে৷
উদাহরণ
সমাধানের কাজ চিত্রিত করার জন্য প্রোগ্রাম,
#include <iostream>
using namespace std;
typedef struct node {
int data;
struct node* left;
struct node* right;
node(int d){
data = d;
left = NULL;
right = NULL;
}
} Node;
void printMirrorSum(Node* root, Node* rootMirror){
if (root->left == NULL && rootMirror->right == NULL)
return;
printMirrorSum(root->left, rootMirror->right);
cout<<(root->left->data + rootMirror->right->data)<<endl;
printMirrorSum(root->right, rootMirror->left);
}
int main(){
Node* root = new Node(1);
root->left = new Node(7);
root->right = new Node(2);
root->left->left = new Node(5);
root->left->right = new Node(8);
root->right->left = new Node(9);
root->right->right = new Node(4);
cout<<"Sum of node and mirror image nodes are :\n";
printMirrorSum(root, root);
if (root)
cout<<(root->data + root->data);
return 0;
} আউটপুট
Sum of node and mirror image nodes are : 9 9 17 2


