এই সমস্যায়, আমাদেরকে N সংখ্যার একটি অ্যারে দেওয়া হয়েছে যেখানে arr[i] (i+1)th নোডকে প্রতিনিধিত্ব করে। এছাড়াও, প্রান্তগুলির M জোড়া রয়েছে যেখানে u এবং v প্রান্ত দ্বারা সংযুক্ত নোডকে উপস্থাপন করে। আমাদের কাজ হল একটি অনির্দেশিত গ্রাফের সমস্ত সংযুক্ত উপাদানগুলিতে ন্যূনতম উপাদানগুলির যোগফল খুঁজে বের করার জন্য একটি প্রোগ্রাম তৈরি করা। যদি একটি নোডের অন্য কোনো নোডের সাথে কোনো সংযোগ না থাকে, তাহলে এটিকে একটি নোডের সাথে একটি উপাদান হিসেবে গণনা করুন।
সমস্যাটি বোঝার জন্য একটি উদাহরণ দেওয়া যাক,
ইনপুট
arr[] = {2, 7, 5, 1, 2} m = 2
1 2
4 5 আউটপুট
8
ব্যাখ্যা
নীচে −
উপরে চিত্রিত গ্রাফ 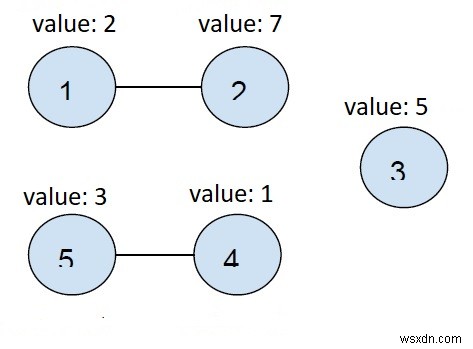
আমাদের দুটি সংযুক্ত নোড এবং একটি একক নোড আছে
সুতরাং, আসুন ন্যূনতম সমস্ত সংযুক্ত উপাদান গ্রহণ করি
মিন (নোড1 এবং নোড2) =মিন (2, 7) =2
মিন (নোড 4 এবং নোড 5) =মিন (1, 3) =1
মিন (নোড৩) =মিনিট (৫) =৫
যোগফল =1 + 2 + 5 =8
এই সমস্যাটি সমাধান করার জন্য, আমরা যেকোনও ট্রাভার্সাল কৌশল (BFS বা DFS) ব্যবহার করে আনডাইরেক্টেড গ্রাফের সমস্ত সংযুক্ত নোডগুলি খুঁজে বের করব এবং তারপরে ভিজিট করা সমস্ত নোডগুলির জন্য একটি ভিজিট করা অ্যারে তৈরি করব যাতে কোনও ডাবল ভিজিট নেই। প্রত্যক্ষ বা পরোক্ষভাবে সংযুক্ত সংযুক্ত নোডগুলি পরিদর্শন করার সময়, আমরা সমস্ত সংযোগের সর্বনিম্ন খুঁজে পাব। এবং thesum ভেরিয়েবলের এই সর্বনিম্ন মান যোগ করুন। আমরা সমস্ত নোড পরিদর্শন করার পরে, আমরা যোগফল প্রিন্ট করব।
উদাহরণ
আমাদের সমাধানের কাজ চিত্রিত করার জন্য প্রোগ্রাম,
#include <bits/stdc++.h>
using namespace std;
const int N = 100;
vector<int> graph[N];
bool visited[N];
void dfs(int node, int arr[], int minimum){
minimum = min(minimum, arr[node]);
visited[node] = true;
for (int i : graph[node]) {
if (!visited[i])
dfs(i, arr, minimum);
}
}
void createEdge(int u, int v){
graph[u - 1].push_back(v - 1);
graph[v - 1].push_back(u - 1);
}
int minSum(int arr[], int n){
int sum = 0;
for (int i = 0; i < n; i++) {
if (!visited[i]) {
int minimum = arr[i];
dfs(i, arr, minimum);
sum += minimum;
}
}
return sum;
}
int main(){
int arr[] = {2, 7, 5, 1, 3};
createEdge(1, 2);
createEdge(4, 5);
int n = sizeof(arr) / sizeof(arr[0]);
cout<<"The sum of minimum elements in all connected components of an undirected graph is ";
cout<<minSum(arr, n);
return 0;
} আউটপুট
The sum of minimum elements in all connected components of an undirected graph is 8


