ধরুন 0 থেকে n-1 পর্যন্ত n বিভিন্ন শহর রয়েছে এবং n-1 রাস্তাও রয়েছে যাতে দুটি ভিন্ন শহরের মধ্যে যাতায়াতের একমাত্র উপায় রয়েছে। ধরুন, পরিবহণ মন্ত্রক রাস্তাগুলিকে এক দিকে অভিমুখ করার সিদ্ধান্ত নিয়েছে কারণ সেগুলি খুব সরু৷
এখানে রাস্তাগুলি সংযোগ দ্বারা প্রতিনিধিত্ব করা হয় যেখানে সংযোগগুলি [i] =[a, b] এটি শহর a থেকে b পর্যন্ত একটি রাস্তাকে প্রতিনিধিত্ব করে৷
রাজধানীতে বড় কোনো অনুষ্ঠান হলে (শহরের সংখ্যা ০) এবং অনেকেই এই শহরে যেতে চান। আমাদের কিছু রাস্তায় কিছু পুনর্বিন্যাস করার কাজ করতে হবে যাতে প্রতিটি শহর শহর 0 পরিদর্শন করতে পারে। আমাদের পরিবর্তিত প্রান্তের ন্যূনতম সংখ্যা খুঁজে বের করতে হবে।
সুতরাং, যদি ইনপুট 6 এর মত হয়, সংযোগ =[[0,1],[1,3],[2,3],[4,0],[4,5]],
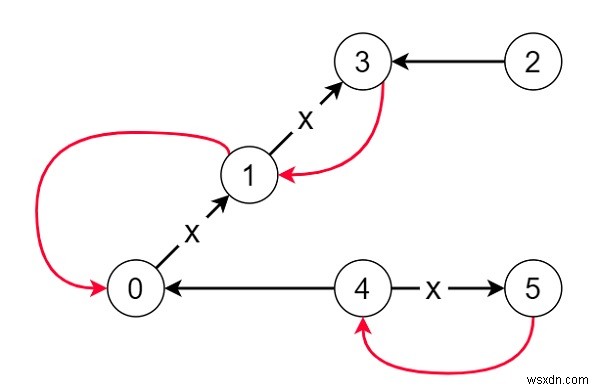
তাহলে আউটপুট হবে 3, কারণ আমাদের লাল রঙে দেখানো প্রান্তের দিক পরিবর্তন করতে হবে যাতে প্রতিটি নোড রাজধানীতে পৌঁছাতে পারে।
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
-
N =5*10^4 + 5
আকারের গ্রাফ1, গ্রাফ2 তালিকার দুটি অ্যারে সংজ্ঞায়িত করুন -
প্রধান পদ্ধতি থেকে নিম্নলিখিতগুলি করুন -
-
-এ একটি মানচিত্র সংজ্ঞায়িত করুন -
প্রতিটি উপাদানের জন্য এটি e, do
-
গ্রাফ1[এটি[0]]
এর শেষে এটি[1] সন্নিবেশ করুন -
গ্রাফ2[এটি[1]]
এর শেষে এটি[0] ঢোকান
-
-
n আকারের একটি অ্যারে ডিস্ট সংজ্ঞায়িত করুন এবং N + 10
দিয়ে এটি পূরণ করুন -
ret :=0, in[0] :=0, dist[0] :=0
-
একটি সারি q
সংজ্ঞায়িত করুন -
q
-এ 0 ঢোকান -
পরিদর্শন করা একটি সেট সংজ্ঞায়িত করুন
-
ভিজিট করা
-এ 0 ঢোকান -
যখন (q খালি নয়), −
করুন-
নোড :=q এর প্রথম উপাদান
-
q
থেকে উপাদান মুছুন -
ret :=ret + dist[নোড]
-
প্রতিটি উপাদানের জন্য এটি গ্রাফ2[নোড], করুন
-
যদি এটি পরিদর্শন না করা হয় এবং dist[it]> 0, তাহলে −
-
dist[it] :=0
-
এটি q
-এ ঢোকান -
ভিজিট করা
এ প্রবেশ করান
-
-
-
প্রতিটি উপাদানের জন্য এটি গ্রাফ1[নোড], করুন
-
যদি এটি পরিদর্শন না করা হয় এবং dist[it]> 1, তাহলে −
-
dist[it] :=1
-
এটি q
-এ ঢোকান -
ভিজিট করা
এ প্রবেশ করান
-
-
-
-
রিটার্ন রিটার্ন
উদাহরণ
আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -
#include <bits/stdc++.h>
using namespace std;
const int N = 5e4 + 5;
class Solution {
public:
vector<int> graph1[N];
vector<int> graph2[N];
int minReorder(int n, vector<vector<int> >& e){
map<int, int> in;
for (auto& it : e) {
graph1[it[0]].push_back(it[1]);
graph2[it[1]].push_back(it[0]);
}
vector<int> dist(n, N + 10);
int ret = 0;
in[0] = 0;
dist[0] = 0;
queue<int> q;
q.push(0);
set<int> visited;
visited.insert(0);
while (!q.empty()) {
int node = q.front();
q.pop();
ret += dist[node];
for (auto& it : graph2[node]) {
if (!visited.count(it) && dist[it] > 0) {
dist[it] = 0;
q.push(it);
visited.insert(it);
}
}
for (auto& it : graph1[node]) {
if (!visited.count(it) && dist[it] > 1) {
dist[it] = 1;
q.push(it);
visited.insert(it);
}
}
}
return ret;
}
};
main(){
Solution ob;
vector<vector<int>> v = {{0,1},{1,3},{2,3},{4,0},{4,5}};
cout << (ob.minReorder(6,v));
} ইনপুট
6,{{0,1},{1,3},{2,3},{4,0},{4,5}} আউটপুট
3


