এই সমস্যায়, আমাদের একটি বাইনারি গাছ বিটি দেওয়া হয়। আমাদের কাজ হল একটি বাইনারি ট্রিতে সর্বাধিক সাব-ট্রি যোগফল খুঁজে বের করার জন্য একটি প্রোগ্রাম তৈরি করা যাতে সাব-ট্রিও একটি BST।
বাইনারি ট্রির একটি বিশেষ শর্ত রয়েছে যে প্রতিটি নোডে সর্বাধিক দুটি সন্তান থাকতে পারে৷
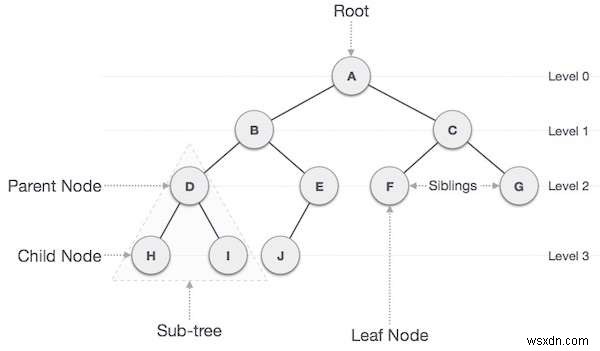
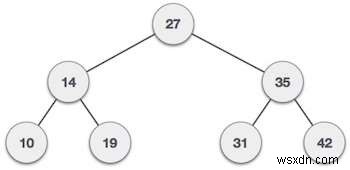
বাইনারি সার্চ ট্রি হল একটি ট্রি যেখানে সমস্ত নোড নিচের উল্লেখিত বৈশিষ্ট্যগুলি অনুসরণ করে
-
বাম সাব-ট্রির কী-এর মান এর মূল (রুট) নোডের কী-এর মানের থেকে কম৷
-
ডান সাবট্রির কী-এর মান তার মূল (রুট) নোডের কী-এর মানের থেকে বেশি বা সমান৷
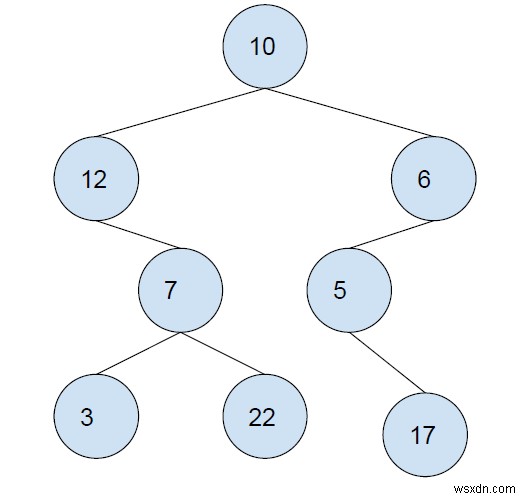
সমস্যাটি বোঝার জন্য একটি উদাহরণ নেওয়া যাক,
ইনপুট
আউটপুট
32
ব্যাখ্যা
এখানে, আমাদের দুটি সাবট্রি আছে যেগুলি BST। তাদের যোগফল হল,
7 + 3 + 22 = 32 6 + 5 + 17 = 28 Maximum = 32.
সমাধান পদ্ধতি
সমস্যার একটি সহজ সমাধান হল ট্রি ডাটা স্ট্রাকচার ট্র্যাভার্স করা এবং তারপর প্রতিটি নোডে চেক করা যে এটি চাইল্ড নোড বাইনারি সার্চ ট্রি তৈরি করতে পারে বা না। যদি আমরা BST-তে অবদানকারী সমস্ত নোডের যোগফল খুঁজে পাই এবং তারপরে পাওয়া সমস্ত BSTSum-এর সর্বাধিক ফেরত দেই।
উদাহরণ
আমাদের সমাধানের কাজ চিত্রিত করার জন্য প্রোগ্রাম,
#include <bits/stdc++.h>
using namespace std;
int findMax(int a, int b){
if(a > b)
return a;
return b;
}
int findMin(int a, int b){
if(a > b)
return b;
return a;
}
struct Node {
struct Node* left;
struct Node* right;
int data;
Node(int data){
this−>data = data;
this−>left = NULL;
this−>right = NULL;
}
};
struct treeVal{
int maxVal;
int minVal;
bool isBST;
int sum;
int currMax;
};
treeVal CalcBSTSumTill(struct Node* root, int& maxsum){
if (root == NULL)
return { −10000, 10000, true, 0, 0 };
if (root−>left == NULL && root−>right == NULL) {
maxsum = findMax(maxsum, root−>data);
return { root−>data, root−>data, true, root−>data, maxsum };
}
treeVal LeftSTree = CalcBSTSumTill(root−>left, maxsum);
treeVal RightSTree = CalcBSTSumTill(root−>right, maxsum);
treeVal currTRee;
if (LeftSTree.isBST && RightSTree.isBST && LeftSTree.maxVal <
root−>data && RightSTree.minVal > root−>data) {
currTRee.maxVal = findMax(root−>data,
findMax(LeftSTree.maxVal, RightSTree.maxVal));
currTRee.minVal = findMin(root−>data,
findMin(LeftSTree.minVal, RightSTree.minVal));
maxsum = findMax(maxsum, RightSTree.sum + root−>data +
LeftSTree.sum);
currTRee.sum = RightSTree.sum + root−>data +
LeftSTree.sum;
currTRee.currMax = maxsum;
currTRee.isBST = true;
return currTRee;
}
currTRee.isBST = false;
currTRee.currMax = maxsum;
currTRee.sum = RightSTree.sum + root−>data + LeftSTree.sum;
return currTRee;
}
int CalcMaxSumBST(struct Node* root){
int maxsum = −10000;
return CalcBSTSumTill(root, maxsum).currMax;
}
int main(){
struct Node* root = new Node(10);
root−>left = new Node(12);
root−>left−>right = new Node(7);
root−>left−>right−>left = new Node(3);
root−>left−>right−>right = new Node(22);
root−>right = new Node(6);
root−>right−>left = new Node(5);
root−>right−>left−>right = new Node(17);
cout<<"The maximum sub−tree sum in a Binary Tree such that the
sub−tree is also a BST is "<<CalcMaxSumBST(root);
return 0;
} আউটপুট
The maximum sub−tree sum in a Binary Tree such that the sub−tree is also a BST is 32


