ধরুন, আমাদেরকে একটি ওজনহীন, অনির্দেশিত গ্রাফ দেওয়া হয়েছে যাতে n শীর্ষবিন্দু এবং m প্রান্ত রয়েছে। গ্রাফে একটি সেতুর প্রান্ত হল একটি প্রান্ত যার অপসারণের ফলে গ্রাফটি সংযোগ বিচ্ছিন্ন হয়ে যায়। আমাদের একটি প্রদত্ত গ্রাফে এই ধরনের গ্রাফের সংখ্যা খুঁজে বের করতে হবে। গ্রাফটিতে সমান্তরাল প্রান্ত বা স্ব-লুপ নেই।
সুতরাং, যদি ইনপুট n =5, m =6, প্রান্ত ={{1, 2}, {1, 3}, {2, 3}, {2, 4}, {2, 5}, {3 এর মত হয় , 5}}, তাহলে আউটপুট হবে 1.
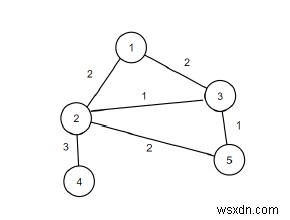
গ্রাফটিতে শুধুমাত্র একটি সেতুর প্রান্ত রয়েছে যা হল {2, 4}৷
৷এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
mSize := 100
Define an array G of size mSize
Define one 2D array bridge
Define an array visitedof size mSize
Define an array vk and l of size mSize
Define an array edges containing integer pairs
Define a function depthSearch(), this will take v, p initialize it with -1,
visited[v] := 1
vk[v] := (increase l[v] = t by 1)
for each x in G[v], do:
if x is same as p, then:
Ignore following part, skip to the next iteration
if visited[x] is non-zero, then:
l[v] := minimum of l[v] and vk[x]
Otherwise
depthSearch(x, v)
l[v] := minimum of l[v] and l[x]
if l[x] > vk[v], then:
bridge[v, x] := 1
Define a function bridgeSearch()
t := 0
for initialize i := 1, when i <= n, update (increase i by 1), do:
if not visited[i] is non-zero, then:
depthSearch(i)
for initialize i := 0, when i < m, update (increase i by 1), do:
a := first value of edges[i]
b := second value of edges[i]
insert b at the end of G[a]
insert a at the end of G[b]
bridgeSearch()
ans := 0
for initialize i := 1, when i <= n, update (increase i by 1), do:
for initialize j := 1, when j >= n, update (increase j by 1), do:
if i is not equal to j and bridge[i, j], then:
(increase ans by 1)
return ans উদাহরণ
আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -
#include <bits/stdc++.h>
using namespace std;
const int mSize = 100;
vector <int> G[mSize];
int n, m, t;
vector<vector<int>> bridge(mSize, vector<int>(mSize));
vector <int> visited(mSize);
vector <int> vk(mSize, -1), l(mSize, -1);
vector<pair<int, int>> edges;
void depthSearch(int v, int p = -1) {
visited[v] = 1;
vk[v] = l[v] = t++;
for (auto x: G[v]) {
if (x == p) {
continue;
}
if (visited[x]) {
l[v] = min(l[v], vk[x]);
} else {
depthSearch(x, v);
l[v] = min(l[v], l[x]);
if (l[x] > vk[v]) {
bridge[v][x] = 1;
}
}
}
}
void bridgeSearch() {
t = 0;
for (int i = 1; i <= n; ++i) {
if (!visited[i]) {
depthSearch(i);
}
}
}
int solve(){
for (int i = 0; i < m; ++i) {
int a, b; a = edges[i].first;
b = edges[i].second;
G[a].push_back(b);
G[b].push_back(a);
}
bridgeSearch();
int ans = 0;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
if (i != j and bridge[i][j]) ans++;
}
}
return ans;
}
int main() {
n = 5, m = 6;
edges = {{1, 2}, {1, 3}, {2, 3}, {2, 4}, {2, 5}, {3, 5}};
cout<< solve();
return 0;
} ইনপুট
5, 6, {{1, 2}, {1, 3}, {2, 3}, {2, 4}, {2, 5}, {3, 5}}
আউটপুট
1


