এই বিভাগে আমরা দেখব স্পারস ম্যাট্রিক্স কী এবং কীভাবে আমরা তাদের মেমরিতে উপস্থাপন করতে পারি। সুতরাং একটি ম্যাট্রিক্স একটি স্পার্স ম্যাট্রিক্স হবে যদি এর বেশিরভাগ উপাদান 0 হয়। আরেকটি সংজ্ঞা হল, সর্বাধিক 1/3 নন-শূন্য উপাদান সহ একটি ম্যাট্রিক্স (মোটামুটি m x n এর 30%) স্পার্স ম্যাট্রিক্স হিসাবে পরিচিত। পি>
আমরা একটি দক্ষ উপায়ে কিছু অপারেশন করতে কম্পিউটারের মেমরিতে ম্যাট্রিক্স ব্যবহার করি। কিন্তু যদি ম্যাট্রিক্সগুলি বিক্ষিপ্ত প্রকৃতির হয়, তবে এটি আমাদের দক্ষতার সাথে অপারেশন করতে সাহায্য করতে পারে, তবে এটি মেমরিতে আরও বড় জায়গা নেবে। যে স্পেস কোন উদ্দেশ্য আছে. তাই আমরা স্পার্স ম্যাট্রিক্স সংরক্ষণ করার জন্য অন্য কিছু ধরণের কাঠামো অনুসরণ করব।
ধরুন আমাদের নিচের মত একটি স্পার্স ম্যাট্রিক্স আছে −
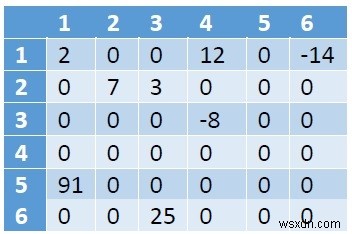
আমরা দেখতে পাচ্ছি যে 8টি অ-শূন্য উপাদান এবং 28টি শূন্য-মান রয়েছে। এই ম্যাট্রিক্স 6*6 =36 মেমরি স্পেস নিচ্ছে। ম্যাট্রিক্সের আকার বড় হলে স্থানের অপচয় বাড়বে।
আমরা টেবিল গঠন ব্যবহার করে স্পার্স ম্যাট্রিক্স সম্পর্কে তথ্য সংরক্ষণ করতে পারি। ধরুন আমরা নিচের মত X নামের একটি টেবিল তৈরি করব -
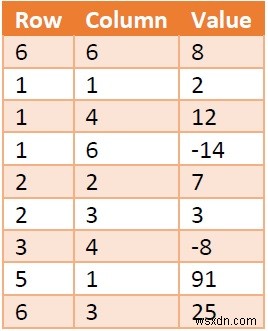
এখানে প্রথম কলামটি সারি নম্বরটি ধরে রেখেছে এবং দ্বিতীয়টি কলাম নম্বরটি ধরে রেখেছে। তৃতীয়টি M[row, col]-এ উপস্থিত ডেটা ধারণ করছে। এই টেবিলের প্রতিটি সারিকে ট্রিপলেট বলা হয়, কারণ তিনটি প্যারামিটার রয়েছে। প্রথম ট্রিপলেটটি ম্যাট্রিক্সের আকারের তথ্য ধারণ করে। সারি =6 এবং কলাম =6 ইঙ্গিত করছে যে ম্যাট্রিক্স M 6 x 6 ম্যাট্রিক্স। মান ক্ষেত্রটি অ্যারেতে উপস্থিত নন-জিরো উপাদানের সংখ্যা নির্দেশ করছে।
এই টেবিলটিও 9*3 =36 পরিমাণ জায়গা নিচ্ছে, তাহলে লাভ কোথায়? ঠিক আছে যদি ম্যাট্রিক্সের আকার 8*8 =64 হয়, কিন্তু শুধুমাত্র 8টি উপাদান থাকে, তাহলেও টেবিল X 36 একক স্থান নেবে। আমরা দেখতে পাচ্ছি যে নির্দিষ্ট 3টি কলাম রয়েছে, সারির সংখ্যা অ-শূন্য উপাদানের সংখ্যার সাথে পরিবর্তিত হয়। তাই যদি অ-শূন্য উপাদানের T সংখ্যা থাকে, তাহলে স্থানের জটিলতা হবে O(3*T) =O(T)। ম্যাট্রিক্সের জন্য এটি হবে O(m x n)।


