গ্রাফ এবং এর উপস্থাপনা

গ্রাফ একটি নন-লিনিয়ার ডেটা স্ট্রাকচার। এটি নোড ব্যবহার করে ডেটা এবং প্রান্তগুলি ব্যবহার করে তাদের সম্পর্ক উপস্থাপন করে। একটি গ্রাফ G এর দুটি বিভাগ রয়েছে। শীর্ষবিন্দু, এবং প্রান্ত. শীর্ষবিন্দুগুলি সেট V ব্যবহার করে উপস্থাপন করা হয়, এবং প্রান্তগুলিকে সেট E হিসাবে উপস্থাপন করা হয়। তাই গ্রাফ স্বরলিপি হল G(V,E)। আসুন ধারণা পেতে একটি উদাহরণ দেখি।

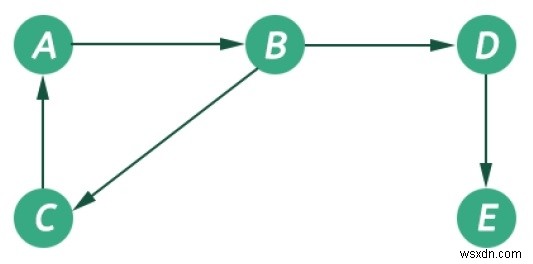
এই গ্রাফে, পাঁচটি শীর্ষবিন্দু এবং পাঁচটি প্রান্ত রয়েছে। প্রান্ত নির্দেশিত হয়. উদাহরণ স্বরূপ, যদি আমরা প্রান্ত সংযোগকারী শীর্ষবিন্দু B এবং D নির্বাচন করি, উৎস শীর্ষবিন্দু B এবং গন্তব্য হল D। তাই আমরা B থেকে D তে যেতে পারি কিন্তু D থেকে B তে যেতে পারি না।

গ্রাফগুলি অ-রৈখিক, এবং এটির কোন নিয়মিত কাঠামো নেই। মেমরিতে একটি গ্রাফ উপস্থাপন করতে, কয়েকটি ভিন্ন শৈলী রয়েছে। এই শৈলী হল −

• সংলগ্ন ম্যাট্রিক্স প্রতিনিধিত্ব
• এজ তালিকা উপস্থাপনা
• সংলগ্ন তালিকা প্রতিনিধিত্ব

সংলগ্ন ম্যাট্রিক্স প্রতিনিধিত্ব

আমরা Adjacency ম্যাট্রিক্স ব্যবহার করে একটি গ্রাফ উপস্থাপন করতে পারি। প্রদত্ত ম্যাট্রিক্স একটি সংলগ্ন ম্যাট্রিক্স। এটি একটি বাইনারি, বর্গাকার ম্যাট্রিক্স এবং ith সারি থেকে jth কলাম পর্যন্ত, যদি একটি প্রান্ত থাকে, তবে সেই স্থানটিকে 1 হিসাবে চিহ্নিত করা হয়। যখন আমরা সংলগ্ন ম্যাট্রিক্স ব্যবহার করে একটি অনির্দেশিত গ্রাফ উপস্থাপন করার চেষ্টা করব, তখন ম্যাট্রিক্সটি প্রতিসম হবে।

এজ তালিকা প্রতিনিধিত্ব

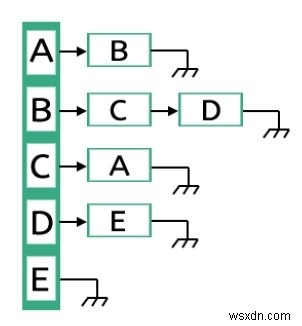
গ্রাফগুলিকে এক মাত্রিক অ্যারে ব্যবহার করেও উপস্থাপন করা যেতে পারে। একে বলা হয় প্রান্ত তালিকা। এই উপস্থাপনায় পাঁচটি প্রান্ত রয়েছে, প্রতিটি প্রান্তের জন্য প্রথম উপাদানটি উত্স এবং দ্বিতীয়টি গন্তব্য। অনির্দেশিত গ্রাফ উপস্থাপনার জন্য প্রান্ত তালিকায় উপাদানের সংখ্যা দ্বিগুণ করা হবে।

সংলগ্ন তালিকা প্রতিনিধিত্ব

এটি অন্য ধরনের গ্রাফ উপস্থাপনা। একে সন্নিহিত তালিকা বলা হয়। এই উপস্থাপনা লিঙ্ক করা তালিকার উপর ভিত্তি করে। এই পদ্ধতিতে, প্রতিটি নোড নোডগুলির একটি তালিকা ধারণ করে, যা সরাসরি সেই শীর্ষবিন্দুগুলির সাথে সংযুক্ত। তালিকার শেষে, প্রতিটি নোড নাল মানগুলির সাথে সংযুক্ত থাকে যাতে বলা হয় যে এটি সেই তালিকার শেষ নোড।