সর্বোত্তম বাইনারি অনুসন্ধান গাছ

পূর্ণসংখ্যার একটি সেট সাজানো ক্রমে দেওয়া হয় এবং ফ্রিকোয়েন্সি গণনা থেকে আরেকটি অ্যারে ফ্রিকোয়েন্সি দেওয়া হয়৷ আমাদের কাজ হল সমস্ত অনুসন্ধানের জন্য সর্বনিম্ন খরচ খুঁজে বের করার জন্য সেই ডেটা দিয়ে একটি বাইনারি অনুসন্ধান ট্রি তৈরি করা৷

উপ-সমস্যাগুলির সমাধান এবং সঞ্চয় করার জন্য একটি সহায়ক অ্যারে খরচ[n, n] তৈরি করা হয়। বটম-আপ পদ্ধতিতে সমস্যা সমাধানের জন্য খরচ ম্যাট্রিক্স ডেটা ধরে রাখবে।

ইনপুট এবং আউটপুট

Input:
The key values as node and the frequency.
Keys = {10, 12, 20}
Frequency = {34, 8, 50}
Output:
The minimum cost is 142.
These are possible BST from the given values.
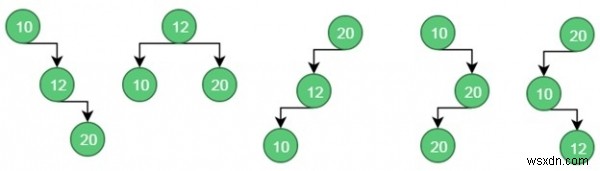For case 1, the cost is: (34*1) + (8*2) + (50*3) = 200
For case 2, the cost is: (8*1) + (34*2) + (50*2) = 176.
Similarly for case 5, the cost is: (50*1) + (34 * 2) + (8 * 3) = 142 (Minimum)

অ্যালগরিদম

optCostBst(keys, freq, n)

ইনপুট: BST-তে সন্নিবেশ করার জন্য কী, প্রতিটি কীর ফ্রিকোয়েন্সি, কীগুলির সংখ্যা।

আউটপুট: সর্বোত্তম BST তৈরির জন্য সর্বনিম্ন খরচ।

Begin
   define cost matrix of size n x n
   for i in range 0 to n-1, do
      cost[i, i] := freq[i]
   done

   for length in range 2 to n, do
      for i in range 0 to (n-length+1), do
         j := i + length – 1
         cost[i, j] := ∞
         for r in range i to j, done
            if r > i, then
               c := cost[i, r-1]
            else
               c := 0
            if r < j, then
               c := c + cost[r+1, j]
            c := c + sum of frequency from i to j
            if c < cost[i, j], then
               cost[i, j] := c
         done
      done
   done
   return cost[0, n-1]
End

উদাহরণ

#include <iostream>
using namespace std;

int sum(int freq[], int low, int high) {    //sum of frequency from low to high range
   int sum = 0;
   for (int k = low; k <=high; k++)
      sum += freq[k];
   return sum;
}

int minCostBST(int keys[], int freq[], int n) {
   int cost[n][n];

   for (int i = 0; i < n; i++)    //when only one key, move along diagonal elements
      cost[i][i] = freq[i];

   for (int length=2; length<=n; length++) {
      for (int i=0; i<=n-length+1; i++) {    //from 0th row to n-length+1 row as i
         int j = i+length-1;
         cost[i][j] = INT_MAX;    //initially store to infinity

         for (int r=i; r<=j; r++) {
            //find cost when r is root of subtree
            int c = ((r > i)?cost[i][r-1]:0)+((r < j)?cost[r+1][j]:0)+sum(freq, i, j);
            if (c < cost[i][j])
               cost[i][j] = c;
         }
      }
   }
   return cost[0][n-1];
}

int main() {
   int keys[] = {10, 12, 20};
   int freq[] = {34, 8, 50};
   int n = 3;
   cout << "Cost of Optimal BST is: "<< minCostBST(keys, freq, n);
}

আউটপুট

Cost of Optimal BST is: 142