সর্বোচ্চ দ্বিপক্ষীয় ম্যাচিং

দ্বিপক্ষীয় ম্যাচিং হল একটি গ্রাফের প্রান্তগুলির একটি সেট এমনভাবে নির্বাচন করা হয় যাতে সেই সেটের দুটি প্রান্ত একটি শেষবিন্দু ভাগ করবে না৷ সর্বাধিক মিল হচ্ছে প্রান্তের সর্বাধিক সংখ্যার সাথে মিলছে৷

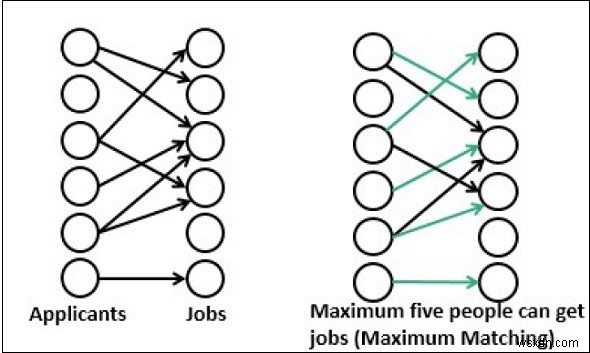
সর্বাধিক মিল পাওয়া গেলে, আমরা অন্য প্রান্ত যোগ করতে পারি না। সর্বোচ্চ মিলে যাওয়া গ্রাফে যদি একটি প্রান্ত যোগ করা হয়, তাহলে সেটি আর মিলবে না। একটি দ্বিপক্ষীয় গ্রাফের জন্য, একাধিক সর্বোচ্চ মিল থাকতে পারে।

ইনপুট এবং আউটপুট

Input:
The adjacency matrix.
0 1 1 0 0 0
1 0 0 1 0 0
0 0 1 0 0 0
0 0 1 1 0 0
0 0 0 0 0 0
0 0 0 0 0 1

Output:
Maximum number of applicants matching for job: 5

অ্যালগরিদম

bipartiteMatch(u, visited, assign)

ইনপুট: স্টার্টিং নোড, ট্র্যাক রাখতে ভিজিট করা তালিকা, অন্য নোডের সাথে নোড অ্যাসাইন করার জন্য তালিকা বরাদ্দ করুন।

আউটপুট - vertex u এর জন্য একটি মিল সম্ভব হলে সত্য ফেরত দেয়।

Begin
   for all vertex v, which are adjacent with u, do
      if v is not visited, then
         mark v as visited
         if v is not assigned, or bipartiteMatch(assign[v], visited, assign) is true, then
            assign[v] := u
            return true
   done
   return false
End

maxMatch(গ্রাফ)

ইনপুট - প্রদত্ত গ্রাফ।

আউটপুট - ম্যাচের সর্বোচ্চ সংখ্যা।

Begin
   initially no vertex is assigned
   count := 0
   for all applicant u in M, do
      make all node as unvisited
      if bipartiteMatch(u, visited, assign), then
         increase count by 1
   done
End

উদাহরণ

#include <iostream>
#define M 6
#define N 6
using namespace std;

bool bipartiteGraph[M][N] = {    //A graph with M applicant and N jobs
   {0, 1, 1, 0, 0, 0},
   {1, 0, 0, 1, 0, 0},
   {0, 0, 1, 0, 0, 0},
   {0, 0, 1, 1, 0, 0},
   {0, 0, 0, 0, 0, 0},
   {0, 0, 0, 0, 0, 1}
};

bool bipartiteMatch(int u, bool visited[], int assign[]) {
   for (int v = 0; v < N; v++) {    //for all jobs 0 to N-1
      if (bipartiteGraph[u][v] && !visited[v]) {    //when job v is not visited and u is interested
         visited[v] = true;    //mark as job v is visited
         //when v is not assigned or previously assigned
         if (assign[v] < 0 || bipartiteMatch(assign[v], visited, assign)) {
            assign[v] = u;    //assign job v to applicant u
            return true;
         }
      }
   }
   return false;
}

int maxMatch() {
   int assign[N];    //an array to track which job is assigned to which applicant
   for(int i = 0; i<N; i++)
      assign[i] = -1;    //initially set all jobs are available
   int jobCount = 0;

   for (int u = 0; u < M; u++) {    //for all applicants
      bool visited[N];
      for(int i = 0; i<N; i++)
         visited[i] = false;    //initially no jobs are visited
      if (bipartiteMatch(u, visited, assign))    //when u get a job
         jobCount++;
   }
   return jobCount;
}

int main() {
   cout << "Maximum number of applicants matching for job: " << maxMatch();
}

আউটপুট

Maximum number of applicants matching for job: 5