একটি 2D ম্যাট্রিক্সে সর্বোচ্চ সমষ্টি আয়তক্ষেত্র

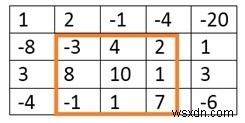
একটি ম্যাট্রিক্স দেওয়া হয়েছে৷ আমাদের একটি আয়তক্ষেত্র (কখনও কখনও বর্গক্ষেত্র) ম্যাট্রিক্স খুঁজে বের করতে হবে, যার যোগফল সর্বাধিক।

এই অ্যালগরিদমের পিছনে ধারণাটি হল বাম এবং ডান কলামগুলি ঠিক করা এবং প্রতিটি সারির জন্য বাম কলাম থেকে ডান কলামে উপাদানের যোগফল খুঁজে বের করার চেষ্টা করা এবং এটি অস্থায়ীভাবে সংরক্ষণ করা। আমরা উপরের এবং নীচের সারি নম্বরগুলি খুঁজে বের করার চেষ্টা করব। অস্থায়ী অ্যারে পাওয়ার পরে, আমরা সর্বাধিক যোগফল সাব-অ্যারে পেতে Kadane এর অ্যালগরিদম প্রয়োগ করতে পারি। এটি দিয়ে, মোট আয়তক্ষেত্র তৈরি হবে।

ইনপুট এবং আউটপুট

Input:
The matrix of integers.
 1  2 -1 -4 -20
-8 -3  4  2   1
 3  8  10 1   3
-4 -1   1 7  -6

Output:
The top left point and bottom right point of the submatrix, and the total sum of the submatrix.
(Top, Left) (1, 1)
(Bottom, Right) (3, 3)
The max sum is: 29

অ্যালগরিদম

কডানে অ্যালগরিদম(অ্যারে, শুরু, শেষ, n)

ইনপুট: অ্যারে যোগফল, শুরু এবং শেষ বিন্দু, উপাদানের সংখ্যা ধারণ করবে।

আউটপুট - শুরু এবং শেষ বিন্দু খুঁজুন।

Begin
   sum := 0 and maxSum := - ∞
   end := -1
   tempStart := 0

   for each element i in the array, do
      sum := sum + array[i]
      if sum < 0, then
         sum := 0
         tempStart := i + 1
      else if sum > maxSum, then
         maxSum := sum
         start := tempStart
         end := i
   done

   if end ≠ -1, then
      return maxSum
   maxSum := array[0], start := 0 and end := 0

   for each element i from 1 to n of array, do
      if array[i] > maxSum, then
         maxSum := array[i]
         start := i and end := i
   done

   return maxSum
End

maxSumRect(ম্যাট্রিক্স)

ইনপুট: প্রদত্ত ম্যাট্রিক্স।

আউটপুট: আয়তক্ষেত্রের সর্বোচ্চ যোগফল।

Begin
   maxSum := - ∞
   define temp array, whose size is same as row of matrix

   for left := 0 to number of columns in the Matrix, do
      till temp array with 0s
      for right := left to column of matrix -1, do
         for each row i, do
            temp[i] := matrix[i, right]
         done

         sum := kadaneAlgorithm(temp, start, end, number of rows)
            if sum > maxSum, then
               maxSum := sum
               endLeft := left
               endRight := right
               endTop := start
               endBottom := end
      done
   done

   display top left and bottom right corner and the maxSum
End

উদাহরণ

#include<iostream>
#define ROW 4
#define COL 5
using namespace std;

int M[ROW][COL] = {
   {1, 2, -1, -4, -20},
   {-8, -3, 4, 2, 1},
   {3, 8, 10, 1, 3},
   {-4, -1, 1, 7, -6}
 };

int kadaneAlgo(int arr[], int &start, int &end, int n) {    //find max sum and starting and ending location
   int sum = 0, maxSum = INT_MIN;

   end = -1;    //at first no place is selected

   int tempStart = 0;    //starting from 0

   for (int i = 0; i < n; i++) {
      sum += arr[i];
      if (sum < 0) {
         sum = 0;
         tempStart = i+1;
      }else if (sum > maxSum) {     //get maximum sum, and update start and end index
         maxSum = sum;
         start = tempStart;
         end = i;
      }
   }

   if (end != -1)
      return maxSum;
   //when all elements are negative in the array
   maxSum = arr[0];
   start = end = 0;

   // Find the maximum element in array
   for (int i = 1; i < n; i++) {
      if (arr[i] > maxSum) {
         maxSum = arr[i];
         start = end = i;
      }
   }
   return maxSum;
}

void maxSumRect() {
   int maxSum = INT_MIN, endLeft, endRight, endTop, endBottom;

   int left, right;
   int temp[ROW], sum, start, end;

   for (left = 0; left < COL; left++) {
      for(int i = 0; i<ROW; i++)//temp initially holds all 0
         temp[i] = 0;

      for (right = left; right < COL; ++right) {
         for (int i = 0; i < ROW; ++i)    //for each row, find the sum
            temp[i] += M[i][right];
         sum = kadaneAlgo(temp, start, end, ROW);    //find sum of rectangle (top, left) and (bottom right)

         if (sum > maxSum) {    //find maximum value of sum, then update corner points
            maxSum = sum;
            endLeft = left;
            endRight = right;
            endTop = start;
            endBottom = end;
         }
      }
   }

   cout << "(Top, Left) ("<<endTop<<", "<<endLeft<<")"<<endl;
   cout << "(Bottom, Right) ("<<endBottom<<", "<<endRight<<")"<<endl;
   cout << "The max sum is: "<< maxSum;
}

int main() {
   maxSumRect();
}

আউটপুট

(Top, Left) (1, 1)
(Bottom, Right) (3, 3)
The max sum is: 29