যে কোন সংখ্যাকে ভাগফল বা ভগ্নাংশ হিসেবে p/q আকারে প্রকাশ করা যায় তাকে মূলদ সংখ্যা বলে। পাইথন লাইব্রেরির ভগ্নাংশ মডিউল মূলদ সংখ্যা পাটিগণিতের জন্য কার্যকারিতা প্রদান করে।
এই মডিউল একটি ভগ্নাংশ শ্রেণী সংজ্ঞায়িত করে। এর অবজেক্টকে নিচের মত বিভিন্ন উপায়ে গঠন করা যেতে পারে -
Fraction(num, denom)
ভগ্নাংশ কনস্ট্রাক্টরের প্রথম সংস্করণ লব এবং হর জন্য দুটি পরামিতি গ্রহণ করে। ডিফল্ট লব হল 0 এবং ডিফল্ট হর হল 1৷ হর-এর মান =0 থ্রো জিরোডিভিশন ত্রুটি৷
>>> from fractions import Fraction >>> n1 = Fraction(2,5) >>> n1 Fraction(2, 5) >>> n2 = Fraction(6,15) >>> n2 Fraction(2, 5) >>> n3 = Fraction(10,1) >>> n3 Fraction(10, 1) >>> n3 = Fraction(10) >>> n3 Fraction(10, 1)
লক্ষ্য করুন যে লব এবং হর পরামিতিগুলিকে সাধারণ গুণনীয়ক দ্বারা ভাগ করার পরে ন্যূনতম মানগুলিতে হ্রাস করা হয়৷
ভগ্নাংশ কনস্ট্রাক্টর স্ট্রিং প্যারামিটারও পেতে পারে যদি এটি বৈধ সাংখ্যিক উপস্থাপনা ধারণ করে।
>>> n1 = Fraction('5')
>>> n1
Fraction(5, 1)
>>> n2 = Fraction('4/7')
>>> n2
Fraction(4, 7)
>>> n3 = Fraction('0.25')
>>> n3
Fraction(1, 4)
>>> n4 = Fraction('1.23E4')
>>> n4
Fraction(12300, 1) একটি ফ্লোটিং পয়েন্ট নম্বরও কনস্ট্রাক্টরের একটি প্যারামিটার হতে পারে। যাইহোক, বিশুদ্ধ বাইনারি আকারে ফ্লোটের প্রতিনিধিত্বের কারণে, লবের ভাগফল এবং ফলস্বরূপ ভগ্নাংশ বস্তুর হর সঠিক নাও হতে পারে। অন্যদিকে, প্যারামিটার হিসাবে দশমিক শ্রেণীর একটি বস্তুও একটি ভগ্নাংশ বস্তু তৈরি করে।
>>> from fractions import Fraction
>>> from decimal import Decimal
>>> n1 = Fraction(2.1)
>>> n1
Fraction(4728779608739021, 2251799813685248)
>>> n2 = Fraction(Decimal('2.1'))
>>> n2
Fraction(21, 10) ভগ্নাংশ বস্তুর সাথে সমস্ত গাণিতিক ক্রিয়াকলাপ অনুমোদিত৷
>>> n1 = Fraction(2,3) >>> n2 = Fraction(1,2) >>> n1+n2 Fraction(7, 6) >>> n1-n2 Fraction(1, 6) >>> n1*n2 Fraction(1, 3) >>> n1/n2 Fraction(4, 3)
শুধু মনে করার জন্য কিভাবে এলোমেলো সংখ্যা পাটিগণিত ভাগফল আকারে সঞ্চালিত হয় −
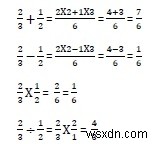
ভগ্নাংশ বস্তুর দুটি বৈশিষ্ট্য আছে, লব এবং হর যা স্বাধীনভাবে অ্যাক্সেস করা যায়।
>>> n1 = Fraction(2,3) >>> n1.numerator 2 >>> n1.denominator 3
ভগ্নাংশ শ্রেণীতে ভাগফলের (ফ্লোর মান) থেকে ছোট বৃহত্তম পূর্ণসংখ্যা এবং ভাগফলের (সিল মান) থেকে বড় একটি ক্ষুদ্রতম পূর্ণসংখ্যা খুঁজে বের করার জন্য নিম্নলিখিত কার্যকর পদ্ধতি রয়েছে
>>> n1 = Fraction(355,113) >>> n1.__floor__() 3 >>> n1.__ceil__() 4
আরেকটি ক্লাস পদ্ধতি limit_denominator() নিকটতম ভগ্নাংশ প্রদান করে যার হরটি নির্দিষ্ট মানের সবচেয়ে সমান।
>>> Fraction('2.71828').limit_denominator(400)
Fraction(1071, 394) এই নিবন্ধে পাইথন স্ট্যান্ডার্ড লাইব্রেরির ভগ্নাংশ মডিউলের বৈশিষ্ট্য এবং ফাংশন নিয়ে আলোচনা করা হয়েছে।


