পাইথন প্রোগ্রামের জন্য কিভাবে একটি প্রদত্ত নম্বর একটি ফিবোনাচি নম্বর কিনা তা পরীক্ষা করবেন?

এই নিবন্ধে, আমরা নীচে দেওয়া সমস্যার বিবৃতিটির সমাধান সম্পর্কে শিখব −

সমস্যা বিবৃতি

একটি সংখ্যা n দেওয়া হয়েছে, পরীক্ষা করুন n একটি ফিবোনাচি সংখ্যা নাকি না

আমরা সবাই জানি যে nম ফিবোনাচি সংখ্যাটি আগের দুটি ফিবোনাচি সংখ্যার যোগফল। কিন্তু তারা পুনরাবৃত্তি সম্পর্ক ছাড়াও একটি আকর্ষণীয় সম্পর্ক অফার করে।

একটি সংখ্যা ফিবোনাচি প্রকৃতির হয় যদি এবং শুধুমাত্র যদি (5*n2 + 4) বা (5*n2 – 4) একটি নিখুঁত বর্গ হয়।

একটি সংখ্যা ফিবোনাচি কিনা তা পরীক্ষা করার জন্য আমরা এই সম্পত্তি ব্যবহার করব৷

এখন পাইথন স্ক্রিপ্ট-

উদাহরণ

ইমপোর্ট ম্যাথ# যদি x হয় নিখুঁত স্কোয়ারডেফ হয় পারফেক্টস্কয়ার(x):s =int(math.sqrt(x)) রিটার্ন s*s ==x# যদি n একটি ফিবিনাচি নম্বরডেফ হয় ফিবোনাচ্চি(n):#যদি 5 এর মধ্যে একটি *n*n + 4 বা 5*n*n - 4 বা উভয়ই একটি পারফেক্ট স্কোয়ার রিটার্ন isPerfectSquare(5*n*n + 4) অথবা isPerfectSquare(5*n*n - 4) রেঞ্জের (1,11) জন্য ):যদি (isFibonacci(i) ==True):print (i," is a Fibonacci Number") else:print (i," is a not Fibonacci Number")

আউটপুট

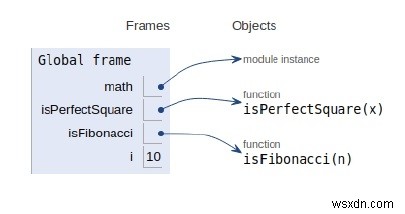
1 হল ফিবোনাচি নম্বর 2 হল ফিবোনাচি নম্বর 3 হল ফিবোনাচি নম্বর 4 হল ফিবোনাচি নয় 5 হল ফিবোনাচি নম্বর 6 হল ফিবোনাচি নম্বর 7 হল ফিবোনাচি নয় নম্বর 8 হল ফিবোনাচি নম্বর 9 হল ফিবোনাচি নম্বর 10 হল ফিবোনাচি নম্বর নয় 

 সমস্ত ফাংশন এবং ভেরিয়েবলগুলিকে গ্লোবাল ফ্রেমে ঘোষণা করা হয়েছে যেমন নীচের ছবিতে দেখানো হয়েছে −
 

 
 
উপসংহার
 

 এই নিবন্ধে, আমরা প্রদত্ত নম্বরটি ফিবোনাচি নাকি না তা সনাক্ত করার সমাধান শিখেছি।