এই নিবন্ধে, আমরা নীচে দেওয়া সমস্যার বিবৃতিটির সমাধান সম্পর্কে জানব৷
সমস্যা বিবৃতি − আমাদের একটি নির্দেশিত গ্রাফ দেওয়া হয়েছে, আমাদের গ্রাফটিতে একটি চক্র আছে কিনা তা পরীক্ষা করতে হবে। প্রদত্ত গ্রাফটিতে কমপক্ষে একটি চক্র থাকলে আউটপুটটি সত্য হওয়া উচিত, অন্যথায় মিথ্যা।
এখন নিচের বাস্তবায়নে সমাধানটি পর্যবেক্ষণ করা যাক -
উদাহরণ
গ্রাফক্লাস গ্রাফ() তৈরির জন্য সংগ্রহ থেকে # সংগ্রহ মডিউল আমদানি ডিফল্টডিক্ট# ক্লাস:# কনস্ট্রাক্টর ডিফ __init__(সেলফ, শীর্ষবিন্দু):self.graph =ডিফল্টডিক্ট(তালিকা) self.V =vertices def addEdge(self, u, v) ):self.graph[u].append(v) def isCyclicUtil(self, v, visited, recStack):# চিহ্নিত করা বর্তমান নোড পরিদর্শন করা এবং রিকারশন স্ট্যাক পরিদর্শন করা যোগ করা[v] =True recStack[v] =True # যদি থাকে প্রতিবেশীকে পরিদর্শন করা হয় এবং recStack-এ তারপর গ্রাফ স্বয়ং প্রতিবেশীর জন্য চক্রাকারে হয়।গ্রাফ[v]:if visited[neighbour] ==False:if self.isCyclicUtil(neighbour, visited, recStack) ==True:return True elif recStack [neighbour] ==True:রিটার্ন True # রিকারশন শেষে নোড পপ করুন recStack[v] =False রিটার্ন False # গ্রাফ সাইক্লিক ডিফ isCyclic(self):ভিজিট করা =[False] * self.V recStack =[False] * self.V রেঞ্জে নোডের জন্য (self.V):if visited[node] ==False:if self.isCyclicUtil(node, visited, recStack) ==True:return True return Falseg =Graph(4)g.addEdge(0, 3)g.addEdge(0, 2)g .addEdge(3, 2)g.addEdge(2, 0)g.addEdge(1, 3)g.addEdge(2, 1) if g.isCyclic() ==1:প্রিন্ট ("গ্রাফ প্রকৃতিতে চক্রাকারে হয়" )else:প্রিন্ট ("গ্রাফ প্রকৃতিতে অ-চক্রীয়")আউটপুট
গ্রাফ প্রকৃতিতে চক্রাকারে
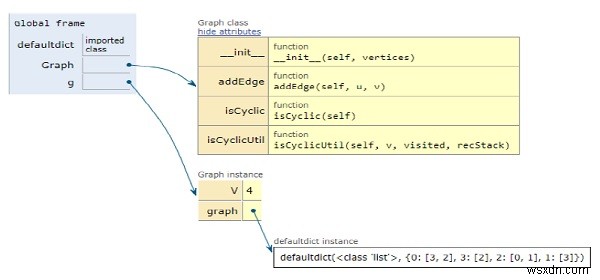
সমস্ত ভেরিয়েবল স্থানীয় সুযোগে ঘোষণা করা হয়েছে এবং তাদের উল্লেখ উপরের চিত্রে দেখা যাচ্ছে।
উপসংহার
এই নিবন্ধে, আমরা কীভাবে একটি নির্দেশিত গ্রাফে সাইকেল সনাক্ত করতে পাইথন প্রোগ্রাম তৈরি করতে পারি সে সম্পর্কে শিখেছি


