এক্সটেন্ডেড ইউক্লিডীয় অ্যালগরিদমের জন্য পাইথন প্রোগ্রাম

এই নিবন্ধে, আমরা নীচে দেওয়া সমস্যার বিবৃতিটির সমাধান সম্পর্কে জানব৷

সমস্যা বিবৃতি − দুটি সংখ্যা দেওয়া হলে আমাদের সেই দুটি সংখ্যার gcd গণনা করতে হবে এবং তাদের প্রদর্শন করতে হবে।

দুটি সংখ্যার GCD সর্বশ্রেষ্ঠ সাধারণ ভাজক হল বৃহত্তম সংখ্যা যা তাদের উভয়কে ভাগ করতে পারে। এখানে আমরা জিসিডি গণনা করার জন্য ইউক্লিডীয় পদ্ধতি অনুসরণ করি অর্থাৎ বারবার সংখ্যাগুলিকে ভাগ করা এবং অবশিষ্টাংশ শূন্য হয়ে গেলে বন্ধ করা। এখানে আমরা পুনরাবৃত্তিতে প্রাপ্ত পূর্ববর্তী মানের উপর ভিত্তি করে অ্যালগরিদম প্রসারিত করি।

এখন নিচের বাস্তবায়নে সমাধানটি পর্যবেক্ষণ করা যাক -

উদাহরণ

# extended Euclidean Algorithm
def gcdExtended(a, b, x, y):
   # Base Case
   if a == 0 :
      x = 0
      y = 1
      return b
   x1 = 1
   y1 = 1 # storing the result
   gcd = gcdExtended(b%a, a, x1, y1)
   # Update x and y with previous calculated values
   x = y1 - (b/a) * x1
   y = x1
   return gcd
x = 1
y = 1
a = 11
b = 15
g = gcdExtended(a, b, x, y)
print("gcd of ", a , "&" , b, " is = ", g)

আউটপুট

gcd of 11 & 15 is = 1

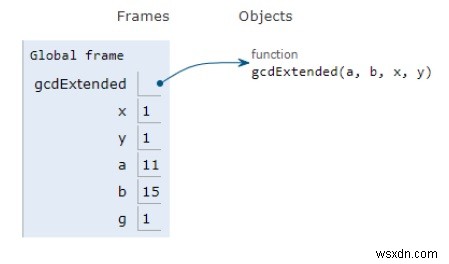
সমস্ত ভেরিয়েবল স্থানীয় সুযোগে ঘোষণা করা হয়েছে এবং তাদের উল্লেখ উপরের চিত্রে দেখা যাচ্ছে।

উপসংহার

এই নিবন্ধে, আমরা কীভাবে এক্সটেন্ডেড ইউক্লিডীয় অ্যালগরিদমের জন্য পাইথন প্রোগ্রাম তৈরি করতে পারি সে সম্পর্কে শিখেছি