পাইথনে রুট থেকে পাতার পথে অপর্যাপ্ত নোড

ধরুন আমাদের একটি বাইনারি গাছ আছে। একটি নোড অপর্যাপ্ত হিসাবে পরিচিত যদি এই নোডটিকে ছেদ করে এমন প্রতিটি মূল থেকে পাতার পথের যোগফল সীমার চেয়ে কঠোরভাবে কম থাকে। আমাদের একই সাথে সমস্ত অপর্যাপ্ত নোড মুছে ফেলতে হবে এবং ফলস্বরূপ বাইনারি গাছের মূলটি ফিরিয়ে দিতে হবে। তাই যদি গাছের মত হয়, এবং সীমা 1 −

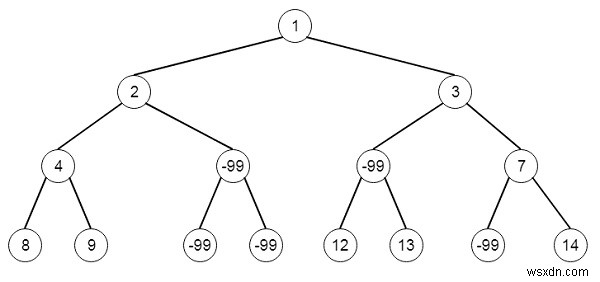
তারপর আউটপুট ট্রি হবে −

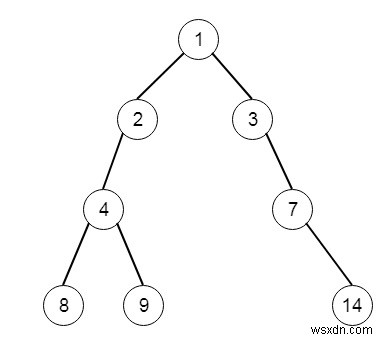
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• একটি পদ্ধতি সংজ্ঞায়িত করুন সমাধান(), এটি রুট এবং সীমাবদ্ধ করবে
• যদি নোডের বাম ও ডান সাবট্রি না থাকে, তাহলে
  • মূলের মান 1-এর কম হলে, শূন্য দিন, অন্যথায় রুট করুন
• যদি রুট-এর বাম সাবট্রি থাকে, তাহলে রুটের বাম :=সমাধান (মূলের বামে, সীমা - মূলের মান)
• যদি রুটের ডান সাবট্রি থাকে, তাহলে রুটের ডানদিকে :=সমাধান (মূলের অধিকার, সীমা - মূলের মান)
• যদি রুটের হয় বাম সাবট্রি, বা ডান সাবট্রি বা উভয়ই, তাহলে রুট রিটার্ন করুন, অন্যথায় শূন্য।

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

উদাহরণ

class Solution(object):
   def sufficientSubset(self, root, limit):
      """
      :type root: TreeNode
      :type limit: int
      :rtype: TreeNode
      """
      if not root.left and not root.right:
         return None if root.val<limit else root
      if root.left:
         root.left= self.sufficientSubset(root.left,limit-root.val)
      if root.right:
         root.right = self.sufficientSubset(root.right,limit-root.val)
      return root if root.left or root.right else None

ইনপুট

[1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14]
1

আউটপুট

[1,2,3,4,null,null,7,8,9,null,14]